Moore plane

In mathematics, the Moore plane, also sometimes called Niemytzki plane (or Nemytskii plane, Nemytskii's tangent disk topology), is a topological space. It is a completely regular Hausdorff space (also called Tychonoff space) which is not normal. It is named after Robert Lee Moore and Viktor Vladimirovich Nemytskii.

Definition

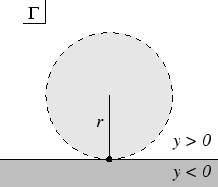
If $\Gamma$ is the (closed) upper half-plane $\Gamma = \{(x,y)\in\R^2 | y \geq 0 \}$, then a topology may be defined on $\Gamma$ by taking a local basis $\mathcal{B}(p,q)$ as follows:

• Elements of the local basis at points $(x,y)$ with $y>0$ are the open discs in the plane which are small enough to lie within $\Gamma$. Thus the subspace topology inherited by $\Gamma\backslash \{(x,0) | x \in \R\}$ is the same as the subspace topology inherited from the standard topology of the Euclidean plane.
• Elements of the local basis at points $p = (x,0)$ are sets $\{p\}\cup A$ where A is an open disc in the upper half-plane which is tangent to the x axis at p.

That is, the local basis is given by

$\mathcal{B}(p,q) = \begin{cases} \{ U_{\epsilon}(p,q):= \{(x,y): (x-p)^2+(y-q)^2 < \epsilon^2 \} \mid \epsilon > 0\}, & \mbox{if } q > 0; \\ \{ V_{\epsilon}(p):= \{(p,0)\} \cup \{(x,y): (x-p)^2+(y-\epsilon)^2 < \epsilon^2 \} \mid \epsilon > 0\}, & \mbox{if } q = 0. \end{cases}$

Properties

• The Moore plane $\Gamma$ is separable, that is, it has a countable dense subset.
• The Moore plane is a completely regular Hausdorff space (i.e. Tychonoff space), which is not normal.
• The subspace $\{(x,0)\in \Gamma | x\in R \}$ of $\Gamma$ has, as its subspace topology, the discrete topology. Thus, the Moore plane shows that a subspace of a separable space need not be separable.
• The Moore plane is first countable, but not second countable or Lindelöf.
• The Moore plane is not locally compact.
• The Moore plane is countably metacompact but not metacompact.

Proof that the Moore plane is not normal

The fact that this space M is not normal can be established by the following counting argument (which is very similar to the argument that the Sorgenfrey plane is not normal):

1. On the one hand, the countable set $S:=\{(p,q) \in \mathbb Q\times \mathbb Q: q>0\}$ of points with rational coordinates is dense in M; hence every continuous function $f:M\to \mathbb R$ is determined by its restriction to $S$, so there can be at most $|\mathbb R|^ {|S|} = 2^{\aleph_0}$ many continuous real-valued functions on M.
2. On the other hand, the real line $L:=\{(p,0): p\in \mathbb R\}$ is a closed discrete subspace of M with $2^{{\aleph _{0}}}$ many points. So there are $2^{2^{\aleph_0}} > 2^{\aleph_0}$ many continuous functions from L to $\mathbb {R}$. Not all these functions can be extended to continuous functions on M.
3. Hence M is not normal, because by the Tietze extension theorem all continuous functions defined on a closed subspace of a normal space can be extended to a continuous function on the whole space.

In fact, if X is a separable topological space having an uncountable closed discrete subspace, X cannot be normal.

See also

• Moore space (disambiguation)
• Hedgehog space

References

• Stephen Willard. General Topology, (1970) Addison-Wesley ISBN 0-201-08707-3.
• Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 507446 (Example 82)
• "Niemytzki plane". PlanetMath.