Neville theta functions

In mathematics, the Neville theta functions, named after Eric Harold Neville,^[1] are defined as follows:^{[2][3] [4]}

$\theta _{c}(z,m)={\sqrt {2}}{\sqrt {\pi }}{\sqrt[ {4}]{q(m)}}\sum _{{k=0}}^{\infty }(q(m))^{{k(k+1)}}\cos \left({\frac 12}\cdot {\frac {(2k+1)\pi z}{K(m)}}\right){\frac {1}{{\sqrt {K(m)}}}}{\frac {1}{{\sqrt[ {4}]{m}}}}$

$\theta _{d}(z,m)=1/2\,{\sqrt {2}}{\sqrt {\pi }}\left(1+2\,\sum _{{k=1}}^{\infty }(q(m))^{{k^{2}}}\cos \left({\frac {\pi zk}{K(m)}}\right)\right){\frac {1}{{\sqrt {K(m)}}}}$

$\theta _{n}(z,m)=1/2\,{\sqrt {\pi }}{\sqrt {2}}\left(1+2\sum _{{k=1}}^{\infty }(-1)^{k}(q(m))^{{k^{2}}}\cos \left({\frac {\pi zk}{K(m)}}\right)\right){\frac {1}{{\sqrt[ {4}]{1-m}}}}{\frac {1}{{\sqrt {K(m)}}}}$

$\theta _{s}(z,m)={\sqrt {\pi }}{\sqrt {2}}{\sqrt[ {4}]{q(m)}}\sum _{{k=0}}^{\infty }(-1)^{k}(q(m))^{{k(k+1)}}\sin \left(1/2\,{\frac {(2k+1)\pi z}{K(m)}}\right){\frac {1}{{\sqrt[ {4}]{1-m}}}}{\frac {1}{{\sqrt[ {4}]{m}}}}{\frac {1}{{\sqrt {K(m)}}}}$

where:

• $K(m)=\operatorname {EllipticK}({\sqrt m})$
• $K'(m)=\operatorname {EllipticK}({\sqrt {1-m}})$
• $q(m)=e^{{-\pi K(m)/K'(m)}}$ is the elliptic nome

Examples

Substitute z = 2.5, m = 0.3 into the above definitions of Neville theta functions(using Maple) once obtain the following(consistent with results from wolfram math).

• $\theta _{c}(2.5,0.3)=-0.65900466676738154967$^[5]
• $\theta _{d}(2.5,0.3)=0.95182196661267561994$
• $\theta _{n}(2.5,0.3)=1.0526693354651613637$
• $\theta _{s}(2.5,0.3)=0.82086879524530400536$

Symmetry

• $\theta _{c}(z,m)=\theta _{c}(-z,m)$
• $\theta _{d}(z,m)=\theta _{d}(-z,m)$
• $\theta _{n}(z,m)=\theta _{n}(-z,m)$
• $\theta _{s}(z,m)=-\theta _{s}(-z,m)$

Complex 3D plots

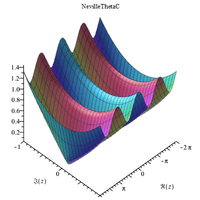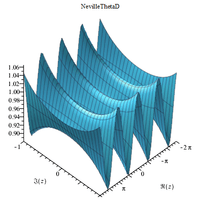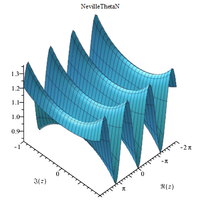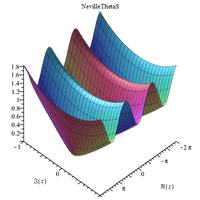Implementation

NetvilleThetaC[z,m], NevilleThetaD[z,m], NevilleThetaN[z,m], and NevilleThetaS[z,m] are built-in functions of Mathematica^[6] No such functions in Maple.

Notes

1. Abramowitz and Stegun, pp. 578-579
2. Neville (1944)
3. wolfram Mathematic
4. wolfram math

References

• Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C., USA; New York, USA: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 0-486-61272-4. LCCN 64-60036. MR 0167642. ISBN 978-0-486-61272-0. LCCN 65-12253.
• Neville, E. H. (Eric Harold) (1944). Jacobian Elliptic Functions. Oxford Clarendon Press.
• Weisstein, Eric W. "Neville Theta Functions". MathWorld.