No-broadcast theorem

In physics, the no-broadcast theorem is a result in quantum information theory. In the case of pure quantum states, it is a corollary of the no-cloning theorem: since quantum states cannot be copied in general, they cannot be broadcast. Here, the word "broadcast" is used in the sense of conveying the state to two or more recipients. For multiple recipients to each receive the state, there must be, in some sense, a way of duplicating the state. The no-broadcast theorem generalizes the no-cloning theorem for mixed states.

The no-cloning theorem says that it is impossible to create two copies of a state given a single copy of the state.

The no-broadcast theorem says that, given a single copy of a state, it is impossible to create a state such that one part of it is the same as the original state and the other part is also the same as the original state. I.e., given an initial state 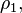$\rho_1,$ it is impossible to create a state 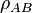$\rho_{AB}$ in a Hilbert space 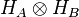$H_A\otimes H_B$ such that the partial trace 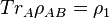$Tr_A\rho_{AB}=\rho_1$ and $Tr_B\rho_{AB}=\rho_1$. 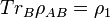Although here we work with mixed states, a broadcasting machine would have to work on any pure state ensemble of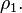 $\rho_1.$

See also

• No-communication theorem
• No-hiding theorem^[1]
• Quantum teleportation
• Quantum entanglement
• Quantum information
• Uncertainty principle
• Transactional interpretation

References

1. Quantum no-hiding theorem experimentally confirmed for first time. Mar 07, 2011 by Lisa Zyga

• Noncommuting Mixed States Cannot Be Broadcast, H. Barnum, C. M. Caves, C. A. Fuchs, R. Jozsa and B. Schumacher, Phys. Rev. Lett. 76, 15, 2818--2821 (1996). (prl.aps.org, ArXiv)