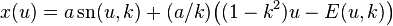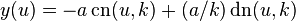Nodary

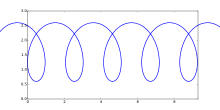
Nodary curve.

In physics and geometry, the nodary is the curve that is traced by the focus of a hyperbola as it rolls without slipping along the axis, a roulette curve. ^[1]

The differential equation of the curve is: $y^2 + \frac{2ay}{\sqrt{1+y'^2}}=b^2$.

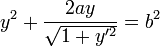Its parametric equation is:

$x(u)=a\operatorname{sn}(u,k)+(a/k)\big((1-k^2)u - E(u,k)\big)$

$y(u)=-a\operatorname{cn}(u,k)+(a/k)\operatorname{dn}(u,k)$

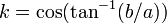where $k= \cos(\tan^{-1}(b/a))$ is the elliptic modulus and 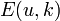$E(u,k)$ is the incomplete elliptic integral of the second kind and sn, cn and dn are Jacobi's elliptic functions.^[1]

The surface of revolution is the nodoid constant mean curvature surface.

References

1. John Oprea, Differential Geometry and its Applications, MAA 2007. pp. 147–148