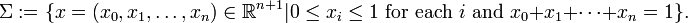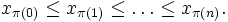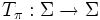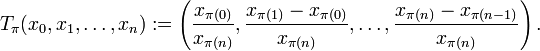Parry–Daniels map
In mathematics, the Parry–Daniels map is a function studied in the context of dynamical systems. Typical questions concern the existence of an invariant or ergodic measure for the map.
It is named after the English mathematician Bill Parry and the British statistician Henry Daniels, who independently studied the map in papers published in 1962.
Definition
Given an integer n ≥ 1, let Σ denote the n-dimensional simplex in Rn+1 given by
Let π be a permutation such that
Then the Parry–Daniels map
is defined by
This article is issued from Wikipedia - version of the 4/20/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.