Pompeiu's theorem

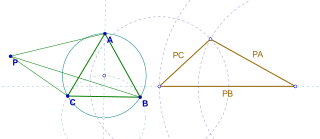
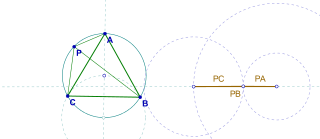
Pompeiu's theorem is a result of plane geometry, discovered by the Romanian mathematician Dimitrie Pompeiu. The theorem is quite simple, but not classical. It states the following:

Given an equilateral triangle ABC in the plane, and a point P in the plane of the triangle ABC, the lengths PA, PB, and PC form the sides of a (maybe, degenerate) triangle.

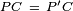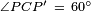The proof is quick. Consider a rotation of 60° about the point C. Assume A maps to B, and P maps to P '. Then we have $\scriptstyle PC\ =\ P'C$, and $\scriptstyle \angle PCP'\ =\ 60^{\circ }$. Hence triangle PCP ' is equilateral and 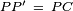$\scriptstyle PP'\ =\ PC$. It is obvious that 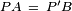$\scriptstyle PA\ =\ P'B$. Thus, triangle PBP ' has sides equal to PA, PB, and PC and the proof by construction is complete.

Further investigations reveal that if P is not in the interior of the triangle, but rather on the circumcircle, then PA, PB, PC form a degenerate triangle, with the largest being equal to the sum of the others.

External links

• MathWorld's page on Pompeiu's Theorem