Quantum mechanical Bell test prediction

In physics, the quantum mechanical Bell test prediction is the prediction that quantum mechanics would give for the correlation probabilities for a set of measurements performed on a quantum entangled state. An important outcome of this prediction is that it violates the Bell inequality, which, as a result, has serious implications for the interpretation of quantum mechanics.

The following is based on section 2 of the Stanford Encyclopedia of Philosophy article written by Abner Shimony, one of the authors of the original Clauser, Horne, Shimony and Holt article (1969) after which the CHSH Bell test is named (Shimony, 2004).

Shimony's derivation of the quantum mechanical prediction

Let the system consist of a pair of photons A and B propagating respectively in the z and −z directions. The two kets |x>j and |y>j constitute a polarization basis for photon j (j =A, B), the former representing (in Dirac's notation) a state in which the photon A is linearly polarized in the x-direction and the latter a state in which it is linearly polarized in the y-direction. For the two-photon system the four product kets |x>A |x>B, |x>A |y>B, |y>A |x>B, and |y>A |y>B constitute a polarization basis. Each two-photon polarization state can be expressed as a linear combination of these four basis states with complex coefficients. Of particular interest are the entangled quantum states, which in no way can be expressed as |α>A|β>B, with |α> and |β> single-photon states, an example being

|Φ> = (1/√2) [ |x>A |x>B + |y>A |y>B ],

 

 

 

 

(1)

which has the useful property of being invariant under rotation of the x and y axes in the plane perpendicular to z. Neither photon A nor photon B is in a definite polarization state when the pair is in the state |Φ>, but their potentialities (in the terminology of Heisenberg 1958) are correlated: if by measurement or some other process the potentiality of photon A to be polarized along the x-direction or along the y-direction is actualized, then the same will be true of photon B, and conversely.

Scheme of a "two-channel" Bell test
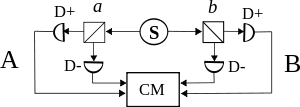
Photon pairs are emitted from the source S, each pair quantum mechanically described by the wave function given in Eq. (1), or by a complete state λ if a local hidden variable theory is assumed. Each photon encounters a two-channel polarization analyzer whose orientation (a or b) can be set by the experimenter. Emerging signals from each channel are detected and coincidences counted by the coincidence monitor CM.

Suppose now that photons A and B impinge respectively on the faces of birefringent crystal polarization analyzers, with the entrance face of each analyzer perpendicular to z. Each analyzer has the property of separating light incident upon its face into two outgoing non-parallel rays, the ordinary ray and the extraordinary ray. The transmission axis of the analyzer is a direction with the property that a photon polarized along it will emerge in the ordinary ray (with certainty if the crystals are assumed to be ideal), while a photon polarized in a direction perpendicular to z and to the transmission axis will emerge in the extraordinary ray. (See diagram.)

The crystals are also idealized by assuming that no incident photon is absorbed, but each emerges in either the '+' or the '−' channel. Quantum mechanics provides an algorithm for computing the probabilities that photons A and B will emerge from these idealized analyzers in specified rays, as functions of the orientations a and b of the analyzers, a being the angle between the transmission axis of the 'A' analyzer and an arbitrary fixed direction in the x–y plane, and b having the analogous meaning for B:

probΦ (j, k |a, b) = | <Φ|θj>A |ξk>B |2.

 

 

 

 

(2a)

Here j is a quantum number associated with the ray into which photon A emerges, taking values +1 or −1 depending on which channel it emerges from, while k is the analogous quantum number for photon B; and | <Φ|θj>A |ξk>B | is the ket representing the quantum state of photons A and B with the respective quantum numbers j and k. Calculation of the probabilities of interest from Eq. (2a) can be simplified by using the invariance noted after Eq. (1) and rewriting |Φ> as

|Φ> = (1/√2) [ |θ1>A |θ1>B + |θ−1>A |θ−1>B ].

 

 

 

 

(3)

Eq. (3) results from Eq. (1) by substituting the transmission axis of the A analyzer for x and the direction perpendicular to both z and this transmission axis for y.

Since |θ−1>A is orthogonal to |θ1>A, only the first term of Eq. (3) contributes to the inner product in Eq. (2a) if j = k = 1; and since the inner product of |θ1>A with itself is unity because of normalization, Eq. (2a) reduces for j = k = 1 to

probΦ (1, 1 |a, b) = 1/2 |  B<θ1 | Φ1>B  |2.

 

 

 

 

(2b)

Finally, the expression on the right hand side of Eq. (2b) is evaluated by using the law of Malus, which is preserved in the quantum mechanical treatment of polarization states: that the probability for a photon polarized in a direction n to pass through an ideal polarization analyzer with axis of transmission n′ equals the squared cosine of the angle between n and n′. Hence

probΦ (1, 1 |a, b) = 1/2 cos2 σ

 

 

 

 

(4a)

where σ is b − a. Likewise,

probΦ (−1, −1 |a, b) = 1/2 cos2 σ,

 

 

 

 

(4b)

and

probΦ (1, −1|a, b) = probΦ (−1, 1|a, b) = 1/2 sin2 σ.

 

 

 

 

(4c)

The expectation value of the product of the results j and k of the polarization analyzes of photons A and B by their respective analyzers is

EΦ (a, b) = probΦ (1, 1 |a, b) + probΦ (−1, −1 |a, b) − probΦ (1, −1 |a, b) − probΦ (−1, 1 |a, b)
= cos2 σ − sin2 σ
= cos 2σ.

 

 

 

 

(5)

The required quantum mechanical predictions are thus 1/2 cos2 σ for coincidence probabilities and cos 2σ for quantum correlations, where σ is the angle between the detectors.

Demonstration of a Bell inequality violation

Now choose as the orientation angles of the transmission axes

a = 0, a′ = π/4, b = π/8, b′ = 3 π/8.

 

 

 

 

(6)

Then

EΦ(a, b) = cos 2(π/8) = 0.707,

 

 

 

 

(7a)

EΦ(a, b′) = cos 2(3π/8) = −0.707,

 

 

 

 

(7b)

EΦ(a′, b) = cos 2(−π/8) = 0.707,

 

 

 

 

(7c)

and

EΦ(a′, b′) = cos 2(π/8) = 0.707.

 

 

 

 

(7d)

Therefore the quantum mechanical prediction for the CHSH test statistic is

SΦ = EΦ(a, b) − EΦ(a, b′) + EΦ(a′, b) + EΦ(a′, b′) = 2.828,

 

 

 

 

(8)

exceeding the CHSH Bell test limit of 2 and thus completing the proof of a version of Bell's Theorem. In fact, all entangled quantum states yield predictions in violation of the inequality, as Gisin (1991) and Popescu and Rohrlich (1992) have independently demonstrated. Popescu and Rohrlich (1992) also show that the maximum amount of violation is achieved with a quantum state of maximum degree of entanglement, exemplified by |Φ> of Eq. (1).

References

This article is issued from Wikipedia - version of the 9/16/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.