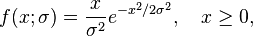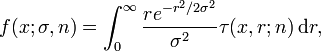Rayleigh mixture distribution

In probability theory and statistics a Rayleigh mixture distribution is a weighted mixture of multiple probability distributions where the weightings are equal to the weightings of a Rayleigh distribution.^[1] Since the probability density function for a (standard) Rayleigh distribution is given by^[2]

$f(x;\sigma) = \frac{x}{\sigma^2} e^{-x^2/2\sigma^2}, \quad x \geq 0,$

Rayleigh mixture distributions have probability density functions of the form

$f(x;\sigma,n) = \int_0^{\infty} \frac{re^{-r^2/2\sigma^2}}{\sigma^2} \tau(x,r;n) \,\mathrm{d}r,$

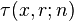where $\tau(x,r;n)$ is a well-defined probability density function or sampling distribution.^[1]

The Rayleigh mixture distribution is one of many types of compound distributions in which the appearance of a value in a sample or population might be interpreted as a function of other underlying random variables. Mixture distributions are often used in mixture models, which are used to express probabilities of sub-populations within a larger population.

See also

• Mixture distribution
• List of probability distributions

References

1. Karim R., Hossain P., Begum S., and Hossain F., "Rayleigh Mixture Distribution", Journal of Applied Mathematics, Vol. 2011, doi:10.1155/2011/238290 (2011).
2. Jackson J.L., "Properties of the Rayleigh Distribution", Johns Hopkins University (1954).