Regular map (graph theory)
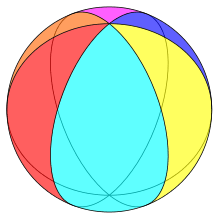
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold such as a sphere, torus, or real projective plane into topological disks, such that every flag (an incident vertex-edge-face triple) can be transformed into any other flag by a symmetry of the decomposition. Regular maps are, in a sense, topological generalizations of Platonic solids. The theory of maps and their classification is related to the theory of Riemann surfaces, hyperbolic geometry, and Galois theory. Regular maps are classified according to either: the genus and orientability of the supporting surface, the underlying graph, or the automorphism group.
Overview
Regular maps are typically defined and studied in three ways: topologically, group-theoretically, and graph-theoretically.
Topological approach
Topologically, a map is a 2-cell decomposition of a closed compact 2-manifold.
The genus g, of a map M is given by Euler's relation which is equal to if the map is orientable, and if the map is non-orientable. It is a crucial fact that there is a finite (non-zero) number of regular maps for every orientable genus except the torus.
Group-theoretical approach
Group-theoretically, the permutation representation of a regular map M is a transitive permutation group C, on a set of flags, generated by three fixed-point free involutions r0, r1, r2 satisfying (r0r2)2= I. In this definition the faces are the orbits of F = <r0, r1>, edges are the orbits of E = <r0, r2>, and vertices are the orbits of V = <r1, r2>. More abstractly, the automorphism group of any regular map is the non-degenerate, homomorphic image of a <2,m,n>-triangle group.
Graph-theoretical approach
Graph-theoretically, a map is a cubic graph with edges coloured blue, yellow, red such that: is connected, every vertex is incident to one edge of each colour, and cycles of edges not coloured blue, have length 4. Note that is the flag graph or graph encoded map (GEM) of the map, defined on the vertex set of flags and is not the skeleton G = (V,E) of the map. In general, || = 4|E|.
A map M is regular iff Aut(M) acts regularly on the flags. Aut(M) of a regular map is transitive on the vertices, edges, and faces of M. A map M is said to be reflexible iff Aut(M) is regular and contains an automorphism that fixes both a vertex v and a face f, but reverses the order of the edges. A map which is regular but not reflexible is said to be chiral.
Examples
- The great dodecahedron is a regular map with pentagonal faces in the orientable surface of genus 4.
- The hemicube is a regular map of type {4,3} in the projective plane. The hemicube, a regular map.
- The hemi-dodecahedron is a regular map produced by pentagonal embedding of the Petersen graph in the projective plane.
- The p-hosohedron is a regular map of type {2,p}. Note that the hosohedra are non-polyhedral in the sense that they are not abstract polytopes. In particular, they do not satisfy the diamond property.
- The Dyck map is a regular map of 12 octagons on a genus-3 surface. Its underlying graph, the Dyck graph, can also form a regular map of 16 hexagons in a torus.
The following is a complete list of regular maps in surfaces of positive Euler characteristic, χ: the sphere and the projective plane.[1].
| χ | g | Schläfli | Vert. | Edges | Faces | Group | Graph | Notes | |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | {p,2} | p | p | 2 | C2 × Dihp | Cp | Dihedron | |
| 2 | 0 | {2,p} | 2 | p | p | C2 × Dihp | p-fold K2 | Hosohedron | |
| 2 | 0 | {3,3} | 4 | 6 | 4 | S4 | K4 | Tetrahedron | |
| 2 | 0 | {4,3} | 8 | 12 | 6 | C2 × S4 | K4 × K2 | Cube | |
| 2 | 0 | {3,4} | 6 | 12 | 8 | C2 × S4 | K2,2,2 | Octahedron | |
| 2 | 0 | {5,3} | 20 | 30 | 12 | C2 × A5 | Dodecahedron | ||
| 2 | 0 | {3,5} | 12 | 30 | 20 | C2 × A5 | K6 × K2 | Icosahedron | |
| 1 | n1 | {2p,2}/2 | p | p | 1 | Dih2p | Cp | Hemi-dihedron[2] | |
| 1 | n1 | {2,2p}/2 | 2 | p | p | Dih2p | p-fold K2 | Hemi-hosohedron[2] | |
| 1 | n1 | {4,3}/2 | 4 | 6 | 3 | S4 | K4 | Hemicube | |
| 1 | n1 | {3,4}/2 | 3 | 6 | 4 | S4 | 2-fold K3 | Hemioctahedron | |
| 1 | n1 | {5,3}/2 | 10 | 15 | 6 | A5 | Petersen graph | Hemidodecahedron | |
| 1 | n1 | {3,5}/2 | 6 | 15 | 10 | A5 | K6 | Hemi-icosahedron | |
The images below show three of the 20 regular maps in the triple torus, labelled with their Schläfli symbols.
-

{6,4}
-

{4,8}
-

{8,4}
See also
- Topological graph theory
- Abstract polytope
- Planar graph
- Toroidal graph
- Graph embedding
- Regular tiling
- Platonic solid
- Platonic graph
References
- ↑ Coxeter (1980)
- 1 2 Séquin, Carlo. "Symmetrical immersions of low-genus non-orientable regular maps" (PDF). Berkeley University.
- Coxeter, H. S. M.; Moser, W. O. J. (1980), Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, 14 (4th ed.), Springer Verlag, ISBN 978-0-387-09212-6.
- van Wijk, Jarke J. (2009), "Symmetric tiling of closed surfaces: visualization of regular maps" (PDF), Proc. SIGGRAPH (ACM Transactions on Graphics), 28 (3): 12, doi:10.1145/1531326.1531355.
- Conder, Marston; Dobcsányi, Peter (2001), "Determination of all regular maps of small genus", Journal of Combinatorial Theory, Series B, 81 (2): 224–242, doi:10.1006/jctb.2000.2008.
- Nedela, Roman (2007), Maps, Hypermaps, and Related Topics (PDF).
- Vince, Andrew (2004), "Maps", Handbook of Graph Theory.
- Brehm, Ulrich; Schulte, Egon (2004), "Polyhedral Maps", Handbook of Discrete and Computational Geometry.