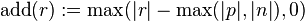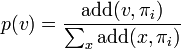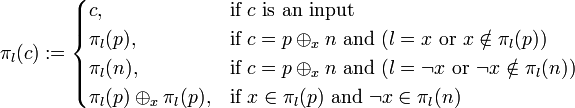Resolution proof compression by splitting
In mathematical logic, proof compression by splitting is an algorithm that operates as a post-process on resolution proofs. It was proposed by Scott Cotton in his paper "Two Techniques for Minimizing Resolution Proof".[1]
The Splitting algorithm is based on the following observation:
Given a proof of unsatisfiability  and a variable
and a variable 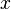 , it is easy to re-arrange (split) the proof in a proof of
, it is easy to re-arrange (split) the proof in a proof of 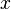 and a proof of
and a proof of 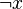 and the recombination of these two proofs (by an additional resolution step) may result in a proof smaller than the original.
and the recombination of these two proofs (by an additional resolution step) may result in a proof smaller than the original.
Note that applying Splitting in a proof 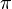 using a variable
using a variable 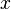 does not invalidates a latter application of the algorithm using a differente variable
does not invalidates a latter application of the algorithm using a differente variable 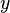 . Actually, the method proposed by Cotton[1] generates a sequence of proofs
. Actually, the method proposed by Cotton[1] generates a sequence of proofs 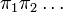 , where each proof
, where each proof 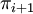 is the result of applying Splitting to
is the result of applying Splitting to 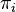 . During the construction of the sequence, if a proof
. During the construction of the sequence, if a proof 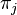 happens to be too large,
happens to be too large, 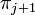 is set to be the smallest proof in
is set to be the smallest proof in 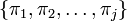 .
.
For achieving a better compression/time ratio, a heuristic for variable selection is desirable. For this purpose, Cotton[1] defines the "additivity" of a resolution step (with antecedents 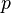 and
and 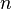 and resolvent
and resolvent  ):
):
Then, for each variable 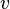 , a score is calculated summing the additivity of all the resolution steps in
, a score is calculated summing the additivity of all the resolution steps in 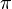 with pivot
with pivot 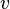 together with the number of these resolution steps. Denoting each score calculated this way by
together with the number of these resolution steps. Denoting each score calculated this way by 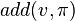 , each variable is selected with a probability proportional to its score:
, each variable is selected with a probability proportional to its score:
To split a proof of unsatisfiability 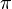 in a proof
in a proof 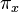 of
of 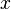 and a proof
and a proof 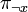 of
of 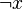 , Cotton [1] proposes the following:
, Cotton [1] proposes the following:
Let 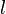 denote a literal and
denote a literal and 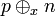 denote the resolvent of clauses
denote the resolvent of clauses 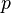 and
and 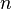 where
where 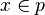 and
and 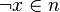 . Then, define the map
. Then, define the map 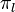 on nodes in the resolution dag of
on nodes in the resolution dag of 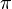 :
:
Also, let 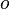 be the empty clause in
be the empty clause in 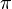 . Then,
. Then, 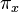 and
and 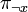 are obtained by computing
are obtained by computing 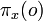 and
and 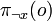 , respectively.
, respectively.