Jensen hierarchy
In set theory, a mathematical discipline, the Jensen hierarchy or J-hierarchy is a modification of Gödel's constructible hierarchy, L, that circumvents certain technical difficulties that exist in the constructible hierarchy. The J-Hierarchy figures prominently in fine structure theory, a field pioneered by Ronald Jensen, for whom the Jensen hierarchy is named.
Definition
As in the definition of L, let Def(X) be the collection of sets definable with parameters over X:
- Def(X) = { {y | y ε X and Φ(y, z1, ..., zn) is true in (X, ε)} | Φ is a first order formula and z1, ..., zn are elements of X}.
The constructible hierarchy, L is defined by transfinite recursion. In particular, at successor ordinals, Lα+1 = Def(Lα).
The difficulty with this construction is that each of the levels is not closed under the formation of unordered pairs; for a given x, y ε Lα+1 − Lα, the set {x,y} will not be an element of Lα+1, since it is not a subset of Lα.
However, Lα does have the desirable property of being closed under Σ0 separation.
Jensen's modified hierarchy retains this property and the slightly weaker condition that 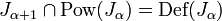 , but is also closed under pairing. The key technique is to encode hereditarily definable sets over Jα by codes; then Jα+1 will contain all sets whose codes are in Jα.
, but is also closed under pairing. The key technique is to encode hereditarily definable sets over Jα by codes; then Jα+1 will contain all sets whose codes are in Jα.
Like Lα, Jα is defined recursively. For each ordinal α, we define 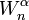 to be a universal Σn predicate for Jα. We encode hereditarily definable sets as
to be a universal Σn predicate for Jα. We encode hereditarily definable sets as 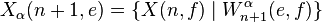 , with
, with 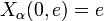 . Then set Jα, n to be {X(n, e) | e in Jα}. Finally, Jα+1 =
. Then set Jα, n to be {X(n, e) | e in Jα}. Finally, Jα+1 = 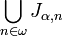 .
.
Properties
Each sublevel Jα, n is transitive and contains all ordinals less than or equal to αω + n. The sequence of sublevels is strictly increasing in n, since a Σm predicate is also Σn for any n > m. The levels Jα will thus be transitive and strictly increasing as well, and are also closed under pairing, Delta-0 comprehension and transitive closure. Moreover, they have the property that
as desired.
The levels and sublevels are themselves Σ1 uniformly definable [i.e. the definition of Jα, n in Jβ does not depend on β], and have a uniform Σ1 well-ordering. Finally, the levels of the Jensen hierarchy satisfy a condensation lemma much like the levels of Godel's original hierarchy.
Rudimentary functions
A rudimentary function is a function that can be obtained from the following operations:
- F(x1, x2, ...) = xi is rudimentary
- F(x1, x2, ...) = {xi, xj} is rudimentary
- F(x1, x2, ...) = xi − xj is rudimentary
- Any composition of rudimentary functions is rudimentary
- ∪z∈yG(z, x1, x2, ...) is rudimentary
For any set M let rud(M) be the smallest set containing M∪{M} closed under the rudimentary operations. Then the Jensen hierarchy satisfies Jα+1 = rud(Jα).
References
- Sy Friedman (2000) Fine Structure and Class Forcing, Walter de Gruyter, ISBN 3-11-016777-8