Seven circles theorem

Seven circles theorem

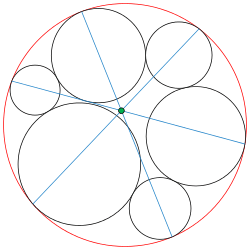
In geometry, the seven circles theorem is a theorem about a certain arrangement of seven circles in the Euclidean plane. Specifically, given a chain of six circles all tangent to a seventh circle and each tangent to its two neighbors, the three lines drawn between opposite pairs of the points of tangency on the seventh circle all pass through the same point. Though elementary in nature, this theorem was not discovered until 1974 (by Evelyn, Money-Coutts, and Tyrrell).

References

• Cundy, H. Martyn (1978). "The seven-circles theorem". The Mathematical Gazette. 62 (421): 200–203. JSTOR 3616692.
• Evelyn, C. J. A.; Money-Coutts, G. B.; Tyrrell, J. A. (1974). The Seven Circles Theorem and Other New Theorems. London: Stacey International. ISBN 978-0-9503304-0-2.
• Wells, D. (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 227–228. ISBN 0-14-011813-6.

External links

• Weisstein, Eric W. "Seven Circles Theorem". MathWorld.

• Interactive Applet by Michael Borcherds showing The Seven Circles Theorem made using GeoGebra.
• the Seven Circles Theorem by Stanley Rabinowitz, with a proof based on Ceva's theorems.
• | Seven Circles Theorem at Cut-the-knot.