Shelah cardinal
In axiomatic set theory, Shelah cardinals are a kind of large cardinals. A cardinal 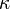 is called Shelah iff for every
is called Shelah iff for every 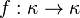 , there exists a transitive class
, there exists a transitive class 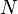 and an elementary embedding
and an elementary embedding 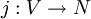 with critical point
with critical point 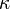 ; and
; and 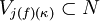 .
.
A Shelah cardinal has a normal ultrafilter containing the set of weakly hyper-Woodin cardinals below it.
References
- Ernest Schimmerling, Woodin cardinals, Shelah cardinals and the Mitchell-Steel core model, Proceedings of the American Mathematical Society 130/11, pp. 3385-3391, 2002, online
This article is issued from Wikipedia - version of the 10/29/2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.