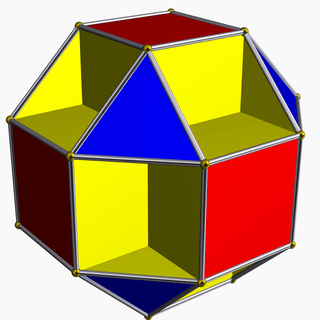
Small cubicuboctahedron

Small cubicuboctahedron
TypeUniform star polyhedron
ElementsF = 20, E = 48
V = 24 (χ = −4)
Faces by sides8{3}+6{4}+6{8}
Wythoff symbol3/2 4 | 4
3 4/3 | 4
Symmetry groupOh, [4,3], *432
Index referencesU13, C38, W69
Dual polyhedronSmall hexacronic icositetrahedron
Vertex figure
4.8.3/2.8
Bowers acronymSocco

In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces (8 triangles, 6 squares, and 6 octagons), 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.

The cubicuboctahedron is a faceting of the rhombicuboctahedron. Its name comes from that the square faces lying on the planes corresponding to the rhombic dodecahedron, has been replaced by six octagonal faces parallel to the square faces of the cube.

It shares the vertex arrangement with the stellated truncated hexahedron. It additionally shares its edge arrangement with the rhombicuboctahedron (having the triangular faces and 6 square faces in common), and with the small rhombihexahedron (having the octagonal faces in common).


Rhombicuboctahedron
Small cubicuboctahedron
Small rhombihexahedron
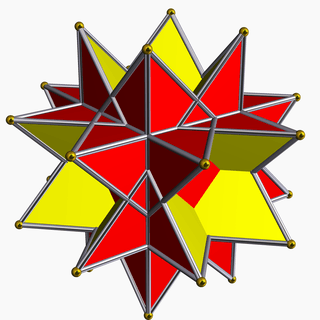Stellated truncated hexahedron
4 tiling is the tiling on the universal cover of the small cubicuboctahedron. (Yellow and red reversed in this tiling, compared to polyhedron.)

As the Euler characteristic suggests, the small cubicuboctahedron is a toroidal polyhedron of genus 3 (topologically it is a surface of genus 3), and thus can be interpreted as a (polyhedral) immersion of a genus 3 polyhedral surface, in the complement of its 24 vertices, into 3-space. (A neighborhood of any vertex is topologically a cone on a figure-8, which cannot occur in an immersion. Note that the Richter reference overlooks this fact.) The underlying polyhedron (ignoring self-intersections) defines a uniform tiling of this surface, and so the small cubicuboctahedron is a uniform polyhedron. In the language of abstract polytopes, the small cubicuboctahedron is a faithful realization of this abstract toroidal polyhedron, meaning that it is a nondegenerate polyhedron and that they have the same symmetry group. In fact, every automorphism of the abstract genus 3 surface with this tiling is realized by an isometry of Euclidean space.

Higher genus surfaces (genus 2 or greater) admit a metric of negative constant curvature (by the uniformization theorem), and the universal cover of the resulting Riemann surface is the hyperbolic plane. The corresponding tiling of the hyperbolic plane has vertex figure 3.8.4.8 (triangle, octagon, square, octagon). If the surface is given the appropriate metric of curvature = −1, the covering map is a local isometry and thus the abstract vertex figure is the same. This tiling may be denoted by the Wythoff symbol 3 4 | 4, and is depicted at right.

The small cubicuboctahedron can also be interpreted as a polyhedral immersion (a coloring of) the Klein quartic,[1] which is a quotient of the order-7 triangular tiling.

Alternatively and more subtly, by chopping up each square face into 2 triangles and each octagonal face into 6 triangles, the small cubicuboctahedron can be interpreted as a non-reglar coloring of the combinatorially regular (not just uniform) tiling of the genus 3 surface by 56 equilateral triangles, meeting at 24 vertices, each with degree 7.[1] This regular tiling is significant as it is a tiling of the Klein quartic, the genus 3 surface with the most symmetric metric (automorphisms of this tiling equal isometries of the surface), and the orientation-preseserving automorphism group of this surface is isomorphic to the projective special linear group PSL(2,7), equivalently GL(3,2) (the order 168 group of all orientation-preserving isometries). Note that the small cubicuboctahedron is not a realization of this abstract polyhedron, as it only has 24 orientation-preserving symmetries (not every abstract automorphism is realized by a Euclidean isometry) – the isometries of the small cubicuboctahedron preserve not only the triangular tiling, but also the coloring, and hence are a proper subgroup of the full isometry group.

The corresponding tiling of the hyperbolic plane (the universal covering) is the order-7 triangular tiling. The automorphism group of the Klein quartic can be augmented (by a symmetry which is not realized by a symmetry of the polyhedron, namely "exchanging the two endpoints of the edges that bisect the squares and octahedra) to yield the Mathieu group M24.[2]

See also

References

  1. 1 2 (Richter) Note each face in the polyhedron consist of multiple faces in the tiling, hence the description as a "coloring" – two triangular faces constitute a square face and so forth, as per this explanatory image.
  2. ↑ (Richter)
This article is issued from Wikipedia - version of the 5/23/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.