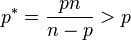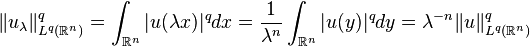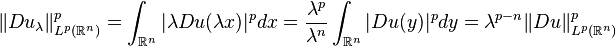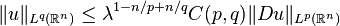Sobolev conjugate
The Sobolev conjugate of p for 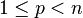 , where n is space dimensionality, is
, where n is space dimensionality, is
This is an important parameter in the Sobolev inequalities.
Motivation
A question arises whether u from the Sobolev space 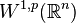 belongs to
belongs to 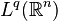 for some q>p. More specifically, when does
for some q>p. More specifically, when does 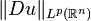 control
control 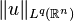 ? It is easy to check that
the following inequality
? It is easy to check that
the following inequality
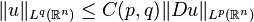 (*)
(*)
can not be true for arbitrary q. Consider 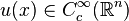 , infinitely differentiable function with compact support. Introduce
, infinitely differentiable function with compact support. Introduce  . We have that
. We have that
The inequality (*) for 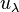 results in the following inequality for
results in the following inequality for 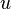
If 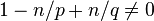 , then by letting
, then by letting 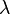 going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for
going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for
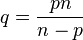 ,
,
which is the Sobolev conjugate.
See also
References
- Lawrence C. Evans. Partial differential equations. Graduate Studies in Mathematics, Vol 19. American Mathematical Society. 1998. ISBN 0-8218-0772-2
This article is issued from Wikipedia - version of the 8/8/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.