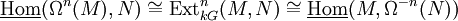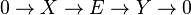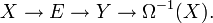Stable module category

In representation theory, the stable module category is a category in which projectives are "factored out."

Definition

Let R be a ring. For two modules M and N, define 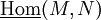$\underline{\mathrm{Hom}}(M,N)$ to be the set of R-linear maps from M to N modulo the relation that f ~ g if f − g factors through a projective module. The stable module category is defined by setting the objects to be the R-modules, and the morphisms are the equivalence classes $\underline{\mathrm{Hom}}(M,N)$.

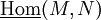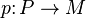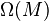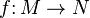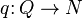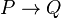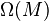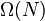Given a module M, let P be a projective module with a surjection $p \colon P \to M$. Then set $\Omega(M)$ to be the kernel of p. Suppose we are given a morphism $f \colon M \to N$ and a surjection $q \colon Q \to N$ where Q is projective. Then one can lift f to a map $P \to Q$ which maps $\Omega(M)$ into $\Omega(N)$. This gives a well-defined functor 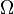$\Omega$ from the stable module category to itself.

For certain rings, such as Frobenius algebras, 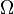$\Omega$ is an equivalence of categories. In this case, the inverse 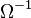$\Omega^{-1}$ can be defined as follows. Given M, find an injective module I with an inclusion 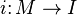$i \colon M \to I$. Then 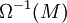$\Omega^{-1}(M)$ is defined to be the cokernel of i. A case of particular interest is when the ring R is a group algebra.

The functor Ω⁻¹ can even be defined on the module category of a general ring (without factoring out projectives), as the cokernel of the injective envelope. It need not be true in this case that the functor Ω⁻¹ is actually an inverse to Ω. One important property of the stable module category is it allows defining the Ω functor for general rings. When R is perfect (or M is finitely generated and R is semiperfect), then Ω(M) can be defined as the kernel of the projective cover, giving a functor on the module category. However, in general projective covers need not exist, and so passing to the stable module category is necessary.

Connections with cohomology

Now we suppose that R = kG is a group algebra for some field k and some group G. One can show that there exist isomorphisms

$\underline{\mathrm{Hom}}(\Omega^n(M), N) \cong \mathrm{Ext}^n_{kG}(M,N) \cong \underline{\mathrm{Hom}}(M, \Omega^{-n}(N))$

for every positive integer n. The group cohomology of a representation M is given by 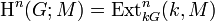$\mathrm{H}^n(G; M) = \mathrm{Ext}^n_{kG}(k, M)$ where k has a trivial G-action, so in this way the stable module category gives a natural setting in which group cohomology lives.

Furthermore, the above isomorphism suggests defining cohomology groups for negative values of n, and in this way, one recovers Tate cohomology.

Triangulated structure

An exact sequence

$0 \to X \to E \to Y \to 0\,$

in the usual module category defines an element of 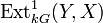$\mathrm{Ext}^1_{kG}(Y,X)$, and hence an element of 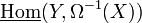$\underline{\mathrm{Hom}}(Y, \Omega^{-1}(X))$, so that we get a sequence

$X \to E \to Y \to \Omega^{-1}(X).\,$

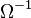Taking $\Omega^{-1}$ to be the translation functor and such sequences as above to be exact triangles, the stable module category becomes a triangulated category.

See also

• Stable homotopy theory

References

• J. F. Carlson, Lisa Townsley, Luis Valero-Elizondo, Mucheng Zhang, Cohomology Rings of Finite Groups, Springer-Verlag, 2003.