Strictly simple group

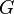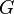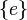In mathematics, in the field of group theory, a group is said to be strictly simple if it has no proper nontrivial ascendant subgroups. That is, $G$ is a strictly simple group if the only ascendant subgroups of $G$ are $\{ e \}$ (the trivial subgroup), and 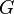$G$ itself (the whole group).

In the finite case, a group is strictly simple if and only if it is simple. However, in the infinite case, strictly simple is a stronger property than simple.

See also

• Serial subgroup
• Absolutely simple group

References

Simple Group Encyclopedia of Mathematics, retrieved 1 January 2012