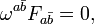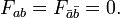Strominger's equations
In heterotic string theory, the Strominger's equations are the set of equations that are necessary and sufficient conditions for spacetime supersymmetry. It is derived by requiring the 4-dimensional spacetime to be maximally symmetric, and adding a warp factor on the internal 6-dimensional manifold.[1]
Consider a metric 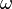 on the real 6-dimensional internal manifold Y and a Hermitian metric h on a vector bundle V. The equations are:
on the real 6-dimensional internal manifold Y and a Hermitian metric h on a vector bundle V. The equations are:
- The 4-dimensional spacetime is Minkowski, i.e.,
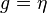 .
. - The internal manifold Y must be complex, i.e., the Nijenhuis tensor must vanish
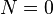 .
. - The Hermitian form
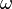 on the complex threefold Y, and the Hermitian metric h on a vector bundle V must satisfy,
on the complex threefold Y, and the Hermitian metric h on a vector bundle V must satisfy,
-
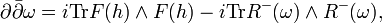
-
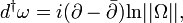
where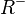 is the Hull-curvature two-form of
is the Hull-curvature two-form of 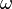 , F is the curvature of h, and
, F is the curvature of h, and 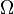 is the holomorphic n-form; F is also known in the physics literature as the Yang-Mills field strength. Li and Yau showed that the second condition is equivalent to
is the holomorphic n-form; F is also known in the physics literature as the Yang-Mills field strength. Li and Yau showed that the second condition is equivalent to 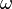 being conformally balanced, i.e.,
being conformally balanced, i.e., 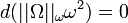 .[2]
.[2]
-
- The Yang-Mills field strength must satisfy,
-
These equations imply the usual field equations, and thus are the only equations to be solved.
However, there are topological obstructions in obtaining the solutions to the equations;
- The second Chern class of the manifold, and the second Chern class of the gauge field must be equal, i.e.,
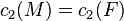
- A holomorphic n-form
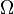 must exists, i.e.,
must exists, i.e., 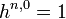 and
and 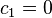 .
.
In case V is the tangent bundle 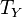 and
and 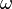 is Kähler, we can obtain a solution of these equations by taking the Calabi-Yau metric on
is Kähler, we can obtain a solution of these equations by taking the Calabi-Yau metric on 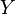 and
and 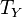 .
.
Once the solutions for the Strominger's equations are obtained, the warp factor 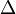 , dilaton
, dilaton 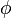 and the background flux H, are determined by
and the background flux H, are determined by
-
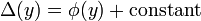 ,
, -
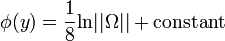 ,
, -
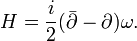
References
- ↑ Strominger, Superstrings with Torsion, Nuclear Physics B274 (1986) 253-284
- ↑ Li and Yau, The Existence of Supersymmetric String Theory with Torsion, J. Differential Geom. Volume 70, Number 1 (2005), 143-181
- Cardoso, Curio, Dall'Agata, Lust, Manousselis, and Zoupanos, Non-Kähler String Backgrounds and their Five Torsion Classes, hep-th/0211118