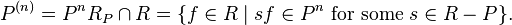Symbolic power of a prime ideal
In algebra, given a ring R and a prime ideal P in it, the n-th symbolic power of P is the ideal
It is the smallest P-primary ideal containing the n-th power Pn. Very roughly, it consists of functions with zeros of order n along the variety defined by P. If R is Noetherian, then it is the P-primary component in the primary decomposition of Pn. We have: 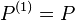 and if P is a maximal ideal, then
and if P is a maximal ideal, then 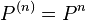 .
.
References
- ↑ Here, by abuse of notation, we write
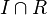 to mean the pre-image of I along the localization map
to mean the pre-image of I along the localization map 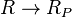 .
.
This article is issued from Wikipedia - version of the 9/16/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.