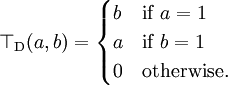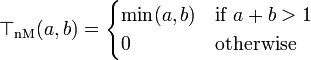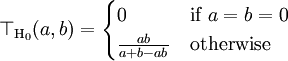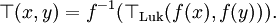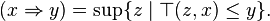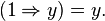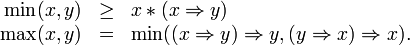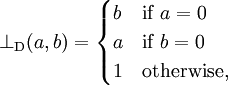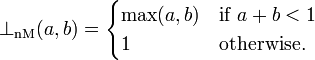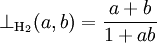T-norm
In mathematics, a t-norm (also T-norm or, unabbreviated, triangular norm) is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic. The name triangular norm refers to the fact that in the framework of probabilistic metric spaces t-norms are used to generalize triangle inequality of ordinary metric spaces.
Definition
A t-norm is a function T: [0, 1] × [0, 1] → [0, 1] which satisfies the following properties:
- Commutativity: T(a, b) = T(b, a)
- Monotonicity: T(a, b) ≤ T(c, d) if a ≤ c and b ≤ d
- Associativity: T(a, T(b, c)) = T(T(a, b), c)
- The number 1 acts as identity element: T(a, 1) = a
Since a t-norm is a binary algebraic operation on the interval [0, 1], infix algebraic notation is also common, with the t-norm usually denoted by 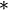 .
.
The defining conditions of the t-norm are exactly those of the partially ordered Abelian monoid on the real unit interval [0, 1]. (Cf. ordered group.) The monoidal operation of any partially ordered Abelian monoid L is therefore by some authors called a triangular norm on L.
Motivations and applications
T-norms are a generalization of the usual two-valued logical conjunction, studied by classical logic, for fuzzy logics. Indeed, the classical Boolean conjunction is both commutative and associative. The monotonicity property ensures that the degree of truth of conjunction does not decrease if the truth values of conjuncts increase. The requirement that 1 be an identity element corresponds to the interpretation of 1 as true (and consequently 0 as false). Continuity, which is often required from fuzzy conjunction as well, expresses the idea that, roughly speaking, very small changes in truth values of conjuncts should not macroscopically affect the truth value of their conjunction.
T-norms are also used to construct the intersection of fuzzy sets or as a basis for aggregation operators (see fuzzy set operations). In probabilistic metric spaces, t-norms are used to generalize triangle inequality of ordinary metric spaces. Individual t-norms may of course frequently occur in further disciplines of mathematics, since the class contains many familiar functions.
Classification of t-norms
A t-norm is called continuous if it is continuous as a function, in the usual interval topology on [0, 1]2. (Similarly for left- and right-continuity.)
A t-norm is called strict if it is continuous and strictly monotone.
A t-norm is called nilpotent if it is continuous and each x in the open interval (0, 1) is its nilpotent element, i.e., there is a natural number n such that x  ...
... 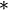 x (n times) equals 0.
x (n times) equals 0.
A t-norm 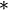 is called Archimedean if it has the Archimedean property, i.e., if for each x, y in the open interval (0, 1) there is a natural number n such that x
is called Archimedean if it has the Archimedean property, i.e., if for each x, y in the open interval (0, 1) there is a natural number n such that x 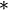 ...
... 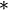 x (n times) is less than or equal to y.
x (n times) is less than or equal to y.
The usual partial ordering of t-norms is pointwise, i.e.,
- T1 ≤ T2 if T1(a, b) ≤ T2(a, b) for all a, b in [0, 1].
As functions, pointwise larger t-norms are sometimes called stronger than those pointwise smaller. In the semantics of fuzzy logic, however, the larger a t-norm, the weaker (in terms of logical strength) conjunction it represents.
Prominent examples

- Minimum t-norm
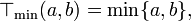 also called the Gödel t-norm, as it is the standard semantics for conjunction in Gödel fuzzy logic. Besides that, it occurs in most t-norm based fuzzy logics as the standard semantics for weak conjunction. It is the pointwise largest t-norm (see the properties of t-norms below).
also called the Gödel t-norm, as it is the standard semantics for conjunction in Gödel fuzzy logic. Besides that, it occurs in most t-norm based fuzzy logics as the standard semantics for weak conjunction. It is the pointwise largest t-norm (see the properties of t-norms below).
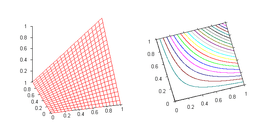
- Product t-norm
 (the ordinary product of real numbers). Besides other uses, the product t-norm is the standard semantics for strong conjunction in product fuzzy logic. It is a strict Archimedean t-norm.
(the ordinary product of real numbers). Besides other uses, the product t-norm is the standard semantics for strong conjunction in product fuzzy logic. It is a strict Archimedean t-norm.

- Łukasiewicz t-norm
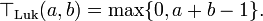 The name comes from the fact that the t-norm is the standard semantics for strong conjunction in Łukasiewicz fuzzy logic. It is a nilpotent Archimedean t-norm, pointwise smaller than the product t-norm.
The name comes from the fact that the t-norm is the standard semantics for strong conjunction in Łukasiewicz fuzzy logic. It is a nilpotent Archimedean t-norm, pointwise smaller than the product t-norm.

- Drastic t-norm
- The name reflects the fact that the drastic t-norm is the pointwise smallest t-norm (see the properties of t-norms below). It is a right-continuous Archimedean t-norm.
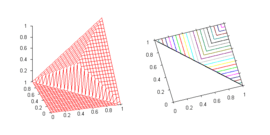
- Nilpotent minimum
- is a standard example of a t-norm which is left-continuous, but not continuous. Despite its name, the nilpotent minimum is not a nilpotent t-norm.
- Hamacher product
- is a strict Archimedean t-norm, and an important representative of the parametric classes of Hamacher t-norms and Schweizer–Sklar t-norms.
Properties of t-norms
The drastic t-norm is the pointwise smallest t-norm and the minimum is the pointwise largest t-norm:
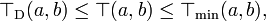 for any t-norm
for any t-norm  and all a, b in [0, 1].
and all a, b in [0, 1].
For every t-norm T, the number 0 acts as null element: T(a, 0) = 0 for all a in [0, 1].
A t-norm T has zero divisors if and only if it has nilpotent elements; each nilpotent element of T is also a zero divisor of T. The set of all nilpotent elements is an interval [0, a] or [0, a), for some a in [0, 1].
Properties of continuous t-norms
Although real functions of two variables can be continuous in each variable without being continuous on [0, 1]2, this is not the case with t-norms: a t-norm T is continuous if and only if it is continuous in one variable, i.e., if and only if the functions fy(x) = T(x, y) are continuous for each y in [0, 1]. Analogous theorems hold for left- and right-continuity of a t-norm.
A continuous t-norm is Archimedean if and only if 0 and 1 are its only idempotents.
A continuous Archimedean t-norm is strict if 0 is its only nilpotent element; otherwise it is nilpotent. By definition, moreover, a continuous Archimedean t-norm T is nilpotent if and only if each x < 1 is a nilpotent element of T. Thus with a continuous Archimedean t-norm T, either all or none of the elements of (0, 1) are nilpotent. If it is the case that all elements in (0, 1) are nilpotent, then the t-norm is isomorphic to the Łukasiewicz t-norm; i.e., there is a strictly increasing function f such that
If on the other hand it is the case that there are no nilpotent elements of T, the t-norm is isomorphic to the product t-norm. In other words, all nilpotent t-norms are isomorphic, the Łukasiewicz t-norm being their prototypical representative; and all strict t-norms are isomorphic, with the product t-norm as their prototypical example. The Łukasiewicz t-norm is itself isomorphic to the product t-norm undercut at 0.25, i.e., to the function p(x, y) = max(0.25, x · y) on [0.25, 1]2.
For each continuous t-norm, the set of its idempotents is a closed subset of [0, 1]. Its complement — the set of all elements which are not idempotent — is therefore a union of countably many non-overlapping open intervals. The restriction of the t-norm to any of these intervals (including its endpoints) is Archimedean, and thus isomorphic either to the Łukasiewicz t-norm or the product t-norm. For such x, y that do not fall into the same open interval of non-idempotents, the t-norm evaluates to the minimum of x and y. These conditions actually give a characterization of continuous t-norms, called the Mostert–Shields theorem, since every continuous t-norm can in this way be decomposed, and the described construction always yields a continuous t-norm. The theorem can also be formulated as follows:
- A t-norm is continuous if and only if it is isomorphic to an ordinal sum of the minimum, Łukasiewicz, and product t-norm.
A similar characterization theorem for non-continuous t-norms is not known (not even for left-continuous ones), only some non-exhaustive methods for the construction of t-norms have been found.
Residuum
For any left-continuous t-norm 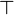 , there is a unique binary operation
, there is a unique binary operation 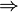 on [0, 1] such that
on [0, 1] such that
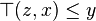 if and only if
if and only if 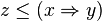
for all x, y, z in [0, 1]. This operation is called the residuum of the t-norm. In prefix notation, the residuum to a t-norm 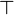 is often denoted by
is often denoted by 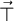 or by the letter R.
or by the letter R.
The interval [0, 1] equipped with a t-norm and its residuum forms a residuated lattice. The relation between a t-norm T and its residuum R is an instance of adjunction: the residuum forms a right adjoint R(x, –) to the functor T(–, x) for each x in the lattice [0, 1] taken as a poset category.
In the standard semantics of t-norm based fuzzy logics, where conjunction is interpreted by a t-norm, the residuum plays the role of implication (often called R-implication).
Basic properties of residua
If 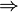 is the residuum of a left-continuous t-norm
is the residuum of a left-continuous t-norm 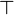 , then
, then
Consequently, for all x, y in the unit interval,
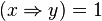 if and only if
if and only if 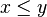
and
If 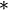 is a left-continuous t-norm and
is a left-continuous t-norm and 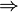 its residuum, then
its residuum, then
If 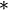 is continuous, then equality holds in the former.
is continuous, then equality holds in the former.
Residua of prominent left-continuous t-norms
If x ≤ y, then R(x, y) = 1 for any residuum R. The following table therefore gives the values of prominent residua only for x > y.
| Residuum of the | Name | Value for x > y | Graph |
|---|---|---|---|
| Minimum t-norm | Standard Gōdel implication | y | 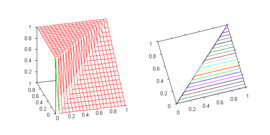 Standard Gödel implication. The function is discontinuous at the line y = x < 1. |
| Product t-norm | Goguen implication | y / x | 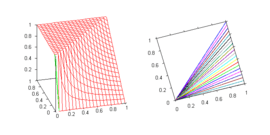 Goguen implication. The function is discontinuous at the point x = y = 0. |
| Łukasiewicz t-norm | Standard Łukasiewicz implication | 1 – x + y |  Standard Łukasiewicz implication. |
| Nilpotent minimum | max(1 – x, y) | 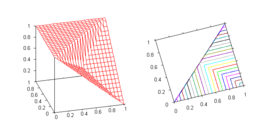 Residuum of the nilpotent minimum. The function is discontinuous at the line 0 < y = x < 1. |
T-conorms
T-conorms (also called S-norms) are dual to t-norms under the order-reversing operation which assigns 1 – x to x on [0, 1]. Given a t-norm, the complementary conorm is defined by
This generalizes De Morgan's laws.
It follows that a t-conorm satisfies the following conditions, which can be used for an equivalent axiomatic definition of t-conorms independently of t-norms:
- Commutativity: ⊥(a, b) = ⊥(b, a)
- Monotonicity: ⊥(a, b) ≤ ⊥(c, d) if a ≤ c and b ≤ d
- Associativity: ⊥(a, ⊥(b, c)) = ⊥(⊥(a, b), c)
- Identity element: ⊥(a, 0) = a
T-conorms are used to represent logical disjunction in fuzzy logic and union in fuzzy set theory.
Examples of t-conorms
Important t-conorms are those dual to prominent t-norms:
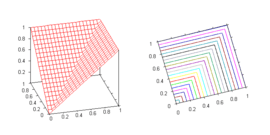
- Maximum t-conorm
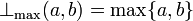 , dual to the minimum t-norm, is the smallest t-conorm (see the properties of t-conorms below). It is the standard semantics for disjunction in Gödel fuzzy logic and for weak disjunction in all t-norm based fuzzy logics.
, dual to the minimum t-norm, is the smallest t-conorm (see the properties of t-conorms below). It is the standard semantics for disjunction in Gödel fuzzy logic and for weak disjunction in all t-norm based fuzzy logics.

- Probabilistic sum
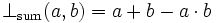 is dual to the product t-norm. In probability theory it expresses the probability of the union of independent events. It is also the standard semantics for strong disjunction in such extensions of product fuzzy logic in which it is definable (e.g., those containing involutive negation).
is dual to the product t-norm. In probability theory it expresses the probability of the union of independent events. It is also the standard semantics for strong disjunction in such extensions of product fuzzy logic in which it is definable (e.g., those containing involutive negation).

- Bounded sum
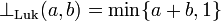 is dual to the Łukasiewicz t-norm. It is the standard semantics for strong disjunction in Łukasiewicz fuzzy logic.
is dual to the Łukasiewicz t-norm. It is the standard semantics for strong disjunction in Łukasiewicz fuzzy logic.
- Drastic t-conorm
- dual to the drastic t-norm, is the largest t-conorm (see the properties of t-conorms below).
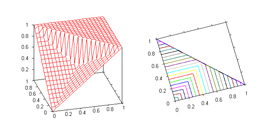
- Nilpotent maximum, dual to the nilpotent minimum:

- Einstein sum (compare the velocity-addition formula under special relativity)
- is a dual to one of the Hamacher t-norms.
Properties of t-conorms
Many properties of t-conorms can be obtained by dualizing the properties of t-norms, for example:
- For any t-conorm ⊥, the number 1 is an annihilating element: ⊥(a, 1) = 1, for any a in [0, 1].
- Dually to t-norms, all t-conorms are bounded by the maximum and the drastic t-conorm:
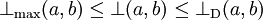 , for any t-conorm
, for any t-conorm  and all a, b in [0, 1].
and all a, b in [0, 1].
Further properties result from the relationships between t-norms and t-conorms or their interplay with other operators, e.g.:
- A t-norm T distributes over a t-conorm S, i.e.,
- T(x, S(y, z)) = S(T(x, y), T(x, z)) for all x, y, z in [0, 1],
- if and only if S is the maximum t-conorm. Dually, any t-conorm distributes over the minimum, but not over any other t-norm.
See also
References
- Klement, Erich Peter; Mesiar, Radko; and Pap, Endre (2000), Triangular Norms. Dordrecht: Kluwer. ISBN 0-7923-6416-3.
- Hájek, Petr (1998), Metamathematics of Fuzzy Logic. Dordrecht: Kluwer. ISBN 0-7923-5238-6
- Cignoli, Roberto L.O.; D'Ottaviano, Itala M.L.; and Mundici, Daniele (2000), Algebraic Foundations of Many-valued Reasoning. Dordrecht: Kluwer. ISBN 0-7923-6009-5
- Fodor, János (2004), "Left-continuous t-norms in fuzzy logic: An overview". Acta Polytechnica Hungarica 1(2), ISSN 1785-8860