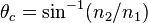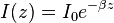Total internal reflection microscopy
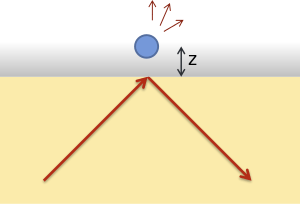
Total internal reflection microscopy is a specialized optical imaging technique for object tracking and detection utilizing the light scattered from an evanescent field in the vicinity of a dielectric interface. Its advantages are a high signal-to-noise ratio and a high spatial resolution in the vertical dimension.
Background
Total internal reflection of light occurs at the interface between materials of differing indices of refraction at incident angles greater than the critical angle, 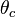 , where
, where
and 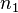 is the index of the incident medium and
is the index of the incident medium and 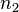 the index of the transmission medium and
the index of the transmission medium and 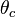 is measured from the normal to the interface.
is measured from the normal to the interface.
Under conditions of total internal reflection, the electromagnetic field in the transmission medium takes on the form of an evanescent wave, whose intensity 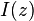 decays exponentially with distance from the interface such that,
decays exponentially with distance from the interface such that,
with 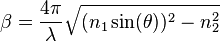 . For practical purposes, the transmission medium is often chosen to be a fluid—usually water—in which a microscopic object can be immersed. The object, when brought close to the interface, is expected to scatter light proportional to the intensity of the field at its height,
. For practical purposes, the transmission medium is often chosen to be a fluid—usually water—in which a microscopic object can be immersed. The object, when brought close to the interface, is expected to scatter light proportional to the intensity of the field at its height, 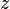 .[1] Since the penetration depth of the evanescent field is on the order of hundreds of nanometers, this technique is among the most sensitive for tracking displacements in the direction perpendicular to a surface.[2]
.[1] Since the penetration depth of the evanescent field is on the order of hundreds of nanometers, this technique is among the most sensitive for tracking displacements in the direction perpendicular to a surface.[2]
Applications
Imaging
The thin excitation region of an evanescent field allows for wide-field imaging of a select sample area with high signal-to-noise ratio. Rather than relying on optical scattering, however, often fluorophores are introduced into the sample for more selective visualization in biological applications. This popular imaging technique is known as a Total internal reflection fluorescence microscopy.
Particle Tracking
Using a calibrated evanescent wave,[1] the position of a colloidal particle or microscopic probe may be tracked with nanometer precision by monitoring the intensity of light scattered via frustrated total internal reflection. Detailed dynamics of the probe or particle can then be obtained, either in thermal equilibrium or non-equilibrium conditions.
For instance, by collecting the time-independent position probability distribution of a probe particle in thermal equilibrium, and inverting the Maxwell–Boltzmann distribution,
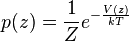 ,
,
where 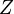 is the partition function, and
is the partition function, and 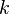 the Boltzmann constant, one can obtain the potential energy profile of interactions between the particle and a surface.[3] In this manner, sub-picoNewton forces may be detected.[4]
the Boltzmann constant, one can obtain the potential energy profile of interactions between the particle and a surface.[3] In this manner, sub-picoNewton forces may be detected.[4]
On the other hand, diffusive dynamics of a cell or a colloid can be deduced from its position time-series obtained via TIRM or another particle-tracking method. Hydrodynamic coupling effects resulting in a particle's reduced diffusion in the vicinity of a solid interface have been studied in this way.[5]
See also
- Total internal reflection fluorescence microscopy
- Evanescent wave
- Total internal reflection
- Dark-field microscopy
References
- 1 2 Prieve, Dennis C., and Nasser A. Frej. "Total internal reflection microscopy: a quantitative tool for the measurement of colloidal forces." Langmuir 6.2 (1990): 396-403.
- ↑ Prieve, Dennis C. "Measurement of colloidal forces with TIRM." Advances in Colloid and Interface Science 82.1 (1999): 93-125.
- ↑ Walz, John Y. "Measuring particle interactions with total internal reflection microscopy." Current opinion in colloid & interface science 2.6 (1997): 600-606.
- ↑ Flicker, Scott G., Jennifer L. Tipa, and Stacy G. Bike. "Quantifying double-layer repulsion between a colloidal sphere and a glass plate using total internal reflection microscopy." Journal of colloid and interface science 158.2 (1993): 317-325.
- ↑ Bevan, Michael A., and Dennis C. Prieve. "Hindered diffusion of colloidal particles very near to a wall: Revisited." The Journal of Chemical Physics 113.3 (2000): 1228-1236.