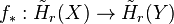Vietoris–Begle mapping theorem

The Vietoris–Begle mapping theorem is a result in the mathematical field of algebraic topology. It is named for Leopold Vietoris and Edward G. Begle. The statement of the theorem, below, is as formulated by Stephen Smale.

Theorem

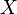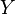Let $X$ and $Y$ be compact metric spaces, and let 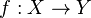$f:X\to Y$ be surjective and continuous. Suppose that the fibers of 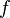$f$ are acyclic, so that

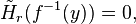$\tilde H_r(f^{-1}(y)) = 0,$ for all 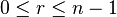$0\leq r\leq n-1$ and all $y\in Y$,

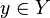with 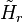$\tilde H_r$ denoting the $r$th reduced homology group. Then, the induced homomorphism

$f_*:\tilde H_r(X)\to\tilde H_r(Y)$

is an isomorphism for 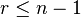$r\leq n-1$ and a surjection for $r=n$.

References

• "Leopold Vietoris (1891–2002)", Notices of the American Mathematical Society, vol. 49, no. 10 (November 2002) by Heinrich Reitberger