Watershed (image processing)
In the study of image processing a watershed of a grayscale image is analogous to the notion of a catchment basin of a heightmap. In short, a drop of water following the gradient of an image flows along a path to finally reach a local minimum. Intuitively, the watershed of a relief correspond to the limits of the adjacent catchment basins of the drops of water.
There are different technical definitions of a watershed. In graphs, watershed lines may be defined on the nodes, on the edges, or hybrid lines on both nodes and edges. Watersheds may also be defined in the continuous domain.[1] There are also many different algorithms to compute watersheds. Watershed algorithm is used in image processing primarily for segmentation purposes.
-

Relief of the gradient magnitude
-
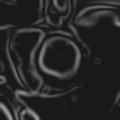
Gradient magnitude image
-
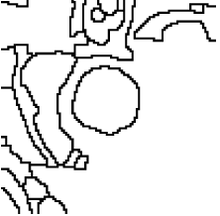
Watershed of the gradient
-

Watershed of the gradient (relief)
Definitions
A watershed is a basin-like landform defined by highpoints and ridgelines that descend into lower elevations and stream valleys.
Watershed by flooding
The idea was introduced in 1979 by S. Beucher and C. Lantuéjoul.[2] The basic idea consisted of placing a water source in each regional minimum in the relief, to flood the entire relief from sources, and build barriers when different water sources meet. The resulting set of barriers constitutes a watershed by flooding.
Watershed by topographic distance
Intuitively, a drop of water falling on a topographic relief flows towards the "nearest" minimum. The "nearest" minimum is that minimum which lies at the end of the path of steepest descent. In terms of topography, this occurs if the point lies in the catchment basin of that minimum. The previous definition does not verify this condition.
Watershed by the drop of water principle
Intuitively, the watershed is a separation of the regional minima from which a drop of water can flow down towards distinct minima. A formalization of this intuitive idea was provided in [3] for defining a watershed of an edge-weighted graph.
Inter-pixel watershed
S. Beucher and F. Meyer introduced an algorithmic inter-pixel implementation of the watershed method,[4] given the following procedure:
1. Label each minimum with a distinct label. Initialize a set S with the labeled nodes.
2. Extract from S a node x of minimal altitude F, that is to say F(x) = min{F(y)|y ∈ S}. Attribute the label of x to each non-labeled node y adjacent to x, and insert y in S.
3. Repeat Step 2 until S is empty.
Topological watershed
Previous notions focus on catchment basins, but not to the produced separating line. The topological watershed was introduced by M. Couprie and G. Bertrand in 1997,[5] and beneficiate of the following fundamental property. A function W is a watershed of a function F if and only if W ≤ F and W preserves the contrast between the regional minima of F; where the contrast between two regional minima M1 and M2 is defined as the minimal altitude to which one must climb in order to go from M1 to M2.[6]
Algorithms
Different approaches may be employed to use the watershed principle for image segmentation.
- Local minima of the gradient of the image may be chosen as markers, in this case an over-segmentation is produced and a second step involves region merging.
- Marker based watershed transformation make use of specific marker positions which have been either explicitly defined by the user or determined automatically with morphological operators or other ways.
Meyer's flooding algorithm
One of the most common watershed algorithms was introduced by F. Meyer in the early 90's.
The algorithm works on a gray scale image. During the successive flooding of the grey value relief, watersheds with adjacent catchment basins are constructed. This flooding process is performed on the gradient image, i.e. the basins should emerge along the edges. Normally this will lead to an over-segmentation of the image, especially for noisy image material, e.g. medical CT data. Either the image must be pre-processed or the regions must be merged on the basis of a similarity criterion afterwards.
- A set of markers, pixels where the flooding shall start, are chosen. Each is given a different label.
- The neighboring pixels of each marked area are inserted into a priority queue with a priority level corresponding to the gradient magnitude of the pixel.
- The pixel with the lowest priority level is extracted from the priority queue. If the neighbors of the extracted pixel that have already been labeled all have the same label, then the pixel is labeled with their label. All non-marked neighbors that are not yet in the priority queue are put into the priority queue.
- Redo step 3 until the priority queue is empty.
The non-labeled pixels are the watershed lines.
Optimal spanning forest algorithms (watershed cuts)
Watersheds as optimal spanning forest have been introduced by Jean Cousty et al.[7] They establish the consistency of these watersheds: they can be equivalently defined by their “catchment basins” (through a steepest descent property) or by the “dividing lines” separating these catchment basins (through the drop of water principle). Then they prove, through an equivalence theorem, their optimality in terms of minimum spanning forests. Afterward, they introduce a linear-time algorithm to compute them. It is worthwhile to note that similar properties are not verified in other frameworks and the proposed algorithm is the most efficient existing algorithm, both in theory and practice.
-

An image with two markers (green), and a Minimum Spanning Forest computed on the gradient of the image.
-

Result of the segmentation by Minimum Spanning Forest
Links with other algorithms in computer vision
Graph cuts
In 2007, C. Allène et al.[8] established links relating Graph Cuts to optimal spanning forests. More precisely, they show that when the power of the weights of the graph is above a certain number, the cut minimizing the graph cuts energy is a cut by maximum spanning forest.
Shortest-path forests
The image foresting transform (IFT) of Falcao et al.[9] is a procedure for computing shortest path forests. It has been proved by J. Cousty et al.[10] that when the markers of the IFT corresponds to extrema of the weight function, the cut induced by the forest is a watershed cut.
Random walker
The random walker algorithm is a segmentation algorithm solving the combinatorial Dirichlet problem, adapted to image segmentation by L. Grady in 2006.[11] In 2009, C. Couprie et al. proved that when the power of the weights of the graph converge toward infinity, the cut minimizing the random walker energy is a cut by maximum spanning forest.[12]
Hierarchies
A hierarchical watershed transformation converts the result into a graph display (i.e. the neighbor relationships of the segmented regions are determined) and applies further watershed transformations recursively.
References
- Fernand Meyer. Un algorithme optimal pour la ligne de partage des eaux. Dans 8me congrès de reconnaissance des formes et intelligence artificielle, Vol. 2 (1991), pages 847–857, Lyon, France.
- Luc Vincent and Pierre Soille. Watersheds in digital spaces: an efficient algorithm based on immersion simulations. In IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 13, Num. 6 (1991), pages 583–598.
- L. Najman and M. Schmitt. Geodesic saliency of watershed contours and hierarchical segmentation. In IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 18, Num. 12 (1996), pages 1163–1173.
- J.B.T.M. Roerdink and A. Meijster. The watershed transform: definitions, algorithms, and parallelization strategies. In Fundamenta Informaticae 41 (2000), pp. 187–228.
- Laurent Najman, Michel Couprie and Gilles Bertrand. Watersheds, mosaics, and the emergence paradigm. In Discrete Applied Mathematics, Vol. 147, Num. 2–3(2005), Pages 301–324.
- ↑ L. Najman and M. Schmitt. Watershed of a continuous function. In Signal Processing (Special issue on Mathematical Morphology.), Vol. 38 (1994), pages 99–112
- ↑ Serge Beucher and Christian Lantuéj workshop on image processing, real-time edge and motion detection (1979). http://cmm.ensmp.fr/~beucher/publi/watershed.pdf
- ↑ J. Cousty, G. Bertrand, L. Najman and M. Couprie. Watershed Cuts: Minimum Spanning Forests and the Drop of Water Principle, Pattern Analysis and Machine Intelligence, IEEE Transactions on 31(8) pp. 1362-1374, 2009,
- ↑ Serge Beucher and Fernand Meyer. The morphological approach to segmentation: the watershed transformation. In Mathematical Morphology in Image Processing (Ed. E. R. Dougherty), pages 433–481 (1993).
- ↑ M. Couprie, G. Bertrand. Topological gray-scale watershed transform. In Proc. of SPIE Vision Geometry V, volume 3168, pages 136–146 (1997). http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.3.7654&rep=rep1&type=pdf
- ↑ G. Bertrand. On topological watersheds. Journal of Mathematical Imaging and Vision, 22(2–3), pages 217–230 (2005).
- ↑ Jean Cousty, Gilles Bertrand, Laurent Najman, and Michel Couprie. Watershed Cuts: Minimum Spanning Forests and the Drop of Water Principle. IEEE Transactions on Pattern Analysis and Machine Intelligence. 31 (8). August 2009. pp. 1362–1374.
- ↑ Cédric Allène, Jean-Yves Audibert, Michel Couprie and Renaud Keriven : "Some links between min-cuts, optimal spanning forests and watersheds", Image and Vision Computing, 2009.
- ↑ Falcao, A.X. Stolfi, J. de Alencar Lotufo, R. : "The image foresting transform: theory, algorithms, and applications", In PAMI, 2004
- ↑ Jean Cousty, Gilles Bertrand, Laurent Najman, and Michel Couprie. Watershed cuts: thinnings, shortest-path forests and topological watersheds. IEEE Transactions on Pattern Analysis and Machine Intelligence. 32 (5). 2010. pp. 925–939.
- ↑ Grady, L.: Random walks for image segmentation. PAMI, 2006
- ↑ C. Couprie, L. Grady, L. Najman and H. Talbot "Power Watersheds: A New Image Segmentation Framework Extending Graph Cuts, Random Walker and Optimal Spanning Forest", ICCV 2009
External links
- The Watershed Transformation with animations of the watershed algorithm.
- Topological Watershed Transform with papers, lecture slides and source code.
- An open source watershed plugin for ImageJ.