Bifolium
For other uses, see Bifolium (disambiguation).
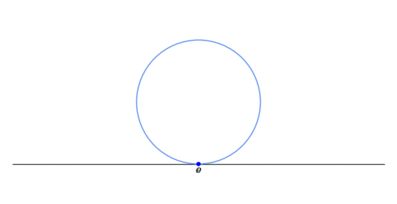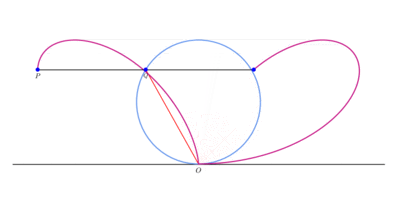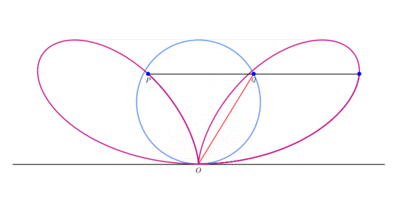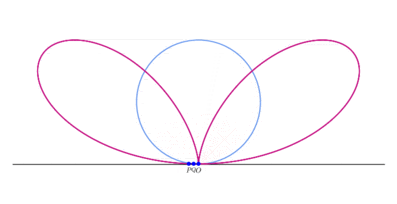
Construction of the Bifolium
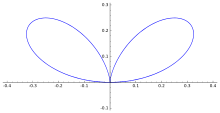
Bifolium for a=1.
Construction and equations
Consider the circle C through the point O, and tangent line L to the circle at point O. For each point Q on C, draw the points P such that PQ is parellel to the tangent line L and PQ = OQ. The collection of points P forms the bifolium.[1]
The bifolium is a quartic plane curve with equation
In polar coordinates, its equation is
References
- ↑ Kokoska, Stephen. "Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers" (PDF).
External links
This article is issued from Wikipedia - version of the 6/4/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.