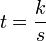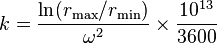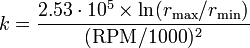Clearing factor

In centrifugation the clearing factor or k factor represents the relative pelleting efficiency of a given centrifuge rotor at maximum rotation speed. It can be used to estimate the time 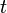$t$ (in hours) required for sedimentation of a fraction with a known sedimentation coefficient $s$ (in svedbergs):

$t = \frac{k}{s}$

The value of the clearing factor depends on the maximum angular velocity 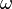$\omega$ of a centrifuge (in rad/s) and the minimum and maximum radius $r$ of the rotor:

$k = \frac{\ln(r_{\rm{max}} / r_{\rm{min}})}{\omega^2} \times \frac{10^{13}}{3600}$

As the rotational speed of a centrifuge is usually specified in RPM, the following formula is often used for convenience:^[1]

$k = \frac{2.53 \cdot 10^5 \times \ln(r_{\rm{max}} / r_{\rm{min}})}{(\rm{RPM}/1000)^2}$

Centrifuge manufacturers usually specify the minimum, maximum and average radius of a rotor, as well as the 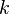$k$ factor of a centrifuge-rotor combination.

For runs with a rotational speed lower than the maximum rotor-speed, the 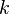$k$ factor has to be adjusted:

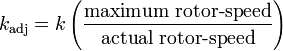$k_{\rm{adj}} = k \left( \frac{\mbox{maximum rotor-speed}}{\mbox{actual rotor-speed}} \right)$²

The K-factor is related to the sedimentation coefficient 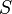$S$ by the formula:

$T = \frac{K}{S}$

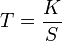
Where 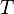$T$ is the time to pellet a certain particle in hours. Since 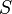$S$ is a constant for a certain particle, this relationship can be used to interconvert between different rotors.

$\frac{T_1}{K_1} = \frac{T_2}{K_2}$

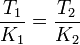
Where 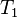$T_1$ is the time to pellet in one rotor, and 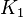$K_1$ is the K-factor of that rotor. 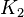$K_2$ is the K-factor of the other rotor, and 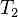$T_2$, the time to pellet in the other rotor, can be calculated. In this manner, one does not need access to the exact rotor cited in a protocol, as long as the K-factor can be calculated. Many online calculators are available to perform the calculations for common rotors.

References

1. "Basics of Centrifugation"

External links

• Beckman Coulter lab resources and manuals
• Appendix F of the Cell Biology Laboratory Manual