Constant function
| Function | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||
| By domain and codomain | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Classes/properties | |||||||||||||||||||||||||||||
| Constant · Identity · Linear · Polynomial · Rational · Algebraic · Analytic · Smooth · Continuous · Measurable · Injective · Surjective · Bijective | |||||||||||||||||||||||||||||
| Constructions | |||||||||||||||||||||||||||||
| Restriction · Composition · λ · Inverse | |||||||||||||||||||||||||||||
| Generalizations | |||||||||||||||||||||||||||||
| Partial · Multivalued · Implicit | |||||||||||||||||||||||||||||
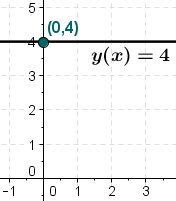
In mathematics, a constant function is a function whose (output) value is the same for every input value.[1][2][3] For example, the function is a constant function because the value of is 4 regardless of the input value (see image).
Basic properties
As a real-valued function of a real-valued argument, a constant function has the general form or just .
- Example: The function or just is the specific constant function where the output value is . The domain of this function is the set of all real numbers ℝ. The codomain of this function is just {2}. The independent variable x does not appear on the right side of the function expression and so its value is "vacuously substituted". Namely y(0)=2, y(−2.7)=2, y(π)=2,.... No matter what value of x is input, the output is "2".
- Real-world example: A store where every item is sold for the price of 1 euro.
The graph of the constant function is a horizontal line in the plane that passes through the point .[4]
In the context of a polynomial in one variable x, the non-zero constant function is a polynomial of degree 0 and its general form is . This function has no intersection point with the x-axis, that is, it has no root (zero). On the other hand, the polynomial is the identically zero function. It is the (trivial) constant function and every x is a root. Its graph is the x-axis in the plane.[5]
A constant function is an even function, i.e. the graph of a constant function is symmetric with respect to the y-axis.
In the context where it is defined, the derivative of a function is a measure of the rate of change of function values with respect to change in input values. Because a constant function does not change, its derivative is 0.[6] This is often written: . The converse is also true. Namely, if y'(x)=0 for all real numbers x, then y(x) is a constant function.[7]
- Example: Given the constant function . The derivative of y is the identically zero function .
Other properties
For functions between preordered sets, constant functions are both order-preserving and order-reversing; conversely, if f is both order-preserving and order-reversing, and if the domain of f is a lattice, then f must be constant.
- Every constant function whose domain and codomain are the same is idempotent.
- Every constant function between topological spaces is continuous.
- A constant function factors through the one-point set, the terminal object in the category of sets. This observation is instrumental for F. William Lawvere's axiomatization of set theory, the Elementary Theory of the Category of Sets (ETCS).[8]
- Every set X is isomorphic to the set of constant functions into it. For each element x and any set Y, there is a unique function such that for all . Conversely, if a function satisfies for all , is by definition a constant function.
- As a corollary, the one-point set is a generator in the category of sets.
- Every set is canonically isomorphic to the function set , or hom set in the category of sets, where 1 is the one-point set. Because of this, and the adjunction between cartesian products and hom in the category of sets (so there is a canonical isomorphism between functions of two variables and functions of one variable valued in functions of another (single) variable, ) the category of sets is a closed monoidal category with the cartesian product of sets as tensor product and the one-point set as tensor unit. In the isomorphisms natural in X, the left and right unitors are the projections and the ordered pairs and respectively to the element , where is the unique point in the one-point set.
A function on a connected set is locally constant if and only if it is constant.
References
- ↑ Tanton, James (2005). Encyclopedia of Mathematics. Facts on File, New York. p. 94. ISBN 0-8160-5124-0.
- ↑ C.Clapham, J.Nicholson (2009). "Oxford Concise Dictionary of Mathematics, Constant Function" (PDF). Addison-Wesley. p. 175. Retrieved January 2014. Check date values in:
|access-date=(help) - ↑ Weisstein, Eric (1999). CRC Concise Encyclopedia of Mathematics. CRC Press, London. p. 313. ISBN 0-8493-9640-9.
- ↑ Dawkins, Paul (2007). "College Algebra". Lamar University. p. 224. Retrieved January 2014. Check date values in:
|access-date=(help) - ↑ Carter, John A.; Cuevas, Gilbert J.; Holliday, Berchie; Marks, Daniel; McClure, Melissa S.publisher=Glencoe/McGraw-Hill School Pub Co (2005). "1". Advanced Mathematical Concepts - Pre-calculus with Applications, Student Edition (1 ed.). p. 22. ISBN 978-0078682278.
- ↑ Dawkins, Paul (2007). "Derivative Proofs". Lamar University. Retrieved January 2014. Check date values in:
|access-date=(help) - ↑ "Zero Derivative implies Constant Function". Retrieved January 2014. Check date values in:
|access-date=(help) - ↑ Leinster, Tom (27 Jun 2011). "An informal introduction to topos theory". arXiv:1012.5647
 [math.CT].
[math.CT].
- Herrlich, Horst and Strecker, George E., Category Theory, Heldermann Verlag (2007).
External links
| Wikimedia Commons has media related to Constant functions. |