Cramér's conjecture

In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936,^[1] is an estimate for the size of gaps between consecutive prime numbers: intuitively, that gaps between consecutive primes are always small, and the conjecture quantifies asymptotically just how small they must be. It states that

$p_{n+1}-p_n=O((\log p_n)^2),\$

where p_n denotes the nth prime number, O is big O notation, and "log" is the natural logarithm. While this is the statement explicitly conjectured by Cramér, his argument actually supports the stronger statement

$\limsup_{n\rightarrow\infty} \frac{p_{n+1}-p_n}{(\log p_n)^2} = 1,$

and this formulation is often called Cramér's conjecture in the literature. However, this stronger formulation is not supported by more accurate heuristic models, which nevertheless support the first version of Cramér's conjecture.

Neither form of Cramér's conjecture has yet been proven or disproven.

Conditional proven results on prime gaps

Cramér gave a conditional proof of the much weaker statement that

$p_{n+1}-p_n = O(\sqrt{p_n}\,\log p_n)$

on the assumption of the Riemann hypothesis.^[1] The best known unconditional bound is

${\displaystyle p_{n+1}-p_{n}=O(p_{n}^{0.525})}$

due to Baker, Harman, and Pintze.^[2]

In the other direction, E. Westzynthius proved in 1931 that prime gaps grow more than logarithmically. That is,^[3]

$\limsup_{n\to\infty}\frac{p_{n+1}-p_n}{\log p_n}=\infty.$

His result was improved by R. A. Rankin,^[4] who proved that

${\displaystyle \limsup _{n\to \infty }{\frac {p_{n+1}-p_{n}}{\log p_{n}\log \log p_{n}\log ^{-2}\log \log p_{n}\log \log \log \log p_{n}}}>0.}$

Paul Erdős conjectured that the left-hand side of the above formula is equal to infinity, and this was proven in 2014 by Kevin Ford, Ben Green, Sergei Konyagin, and Terence Tao.^[5]

Heuristic justification

Cramér's conjecture is based on a probabilistic model (essentially a heuristic) of the primes, in which one assumes that the probability of a natural number of size x being prime is 1/log x. This is known as the Cramér model of the primes.

In the Cramér random model,

${\displaystyle \limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\log ^{2}p_{n}}}=1}$

with probability one.^[1] However, as pointed out by Andrew Granville,^[6] Maier's theorem shows that the Cramér random model does not adequately describe the distribution of primes on short intervals, and a refinement of Cramér's model taking into account divisibility by small primes suggests that $c \ge 2e^{-\gamma}\approx1.1229\ldots$ ( A125313), where $\gamma$ is the Euler–Mascheroni constant. János Pintz has suggested that the limit sup may be infinite,^[7] and similarly Leonard Adleman and Kevin McCurley write

As a result of the work of H. Maier on gaps between consecutive primes, the exact formulation of Cramér's conjecture has been called into question [...] It is still probably true that for every constant $c>2$, there is a constant $d>0$ such that there is a prime between $x$ and ${\displaystyle x+d(\log x)^{c}}$. ^[8]

Related conjectures and heuristics

Prime gap function

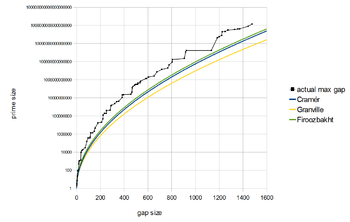
Daniel Shanks conjectured asymptotic equality of record gaps, a somewhat stronger statement than Cramér's conjecture.^[9]

In the paper ^[10] J.H. Cadwell has proposed the formula for the maximal gaps: ${\displaystyle G(x)\sim \log x(\log x-\log \log x),}$ which for large $x$ goes into the Cramer's conjecture ${\displaystyle G(x)\sim \log ^{2}x}$.

Thomas Nicely has calculated many large prime gaps.^[11] He measures the quality of fit to Cramér's conjecture by measuring the ratio

${\displaystyle R={\frac {\log p_{n}}{\sqrt {p_{n+1}-p_{n}}}}.}$

He writes, “For the largest known maximal gaps, $R$ has remained near 1.13.” However, $1/R^{2}$ is still less than 1, and it does not provide support to Granville's refinement that c should be greater than 1.

See also

• Prime number theorem
• Legendre's conjecture and Andrica's conjecture, much weaker but still unproven upper bounds on prime gaps
• Firoozbakht's conjecture
• Maier's theorem on the numbers of primes in short intervals for which the model predicts an incorrect answer

References

1. Cramér, Harald (1936), "On the order of magnitude of the difference between consecutive prime numbers" (PDF), Acta Arithmetica, 2: 23–46
2. R. C. Baker, G. Harman, and J. Pintze, The difference between consecutive primes. II. Proc. London Math. Soc. (3), 83 (2001), no. 3, 532-562
3. Westzynthius, E. (1931), "Über die Verteilung der Zahlen die zu den n ersten Primzahlen teilerfremd sind", Commentationes Physico-Mathematicae Helsingsfors (in German), 5: 1–37, JFM 57.0186.02, Zbl 0003.24601.
4. R. A. Rankin, The difference between consecutive prime numbers, J. London Math. Soc. 13 (1938), 242-247
5. K. Ford, B. Green, S. Konyagin, and T. Tao, Large gaps between consecutive prime numbers. Ann. of Math. (2) 183 (2016), no. 3, 935–974
6. Granville, A. (1995), "Harald Cramér and the distribution of prime numbers" (PDF), Scandinavian Actuarial Journal, 1: 12–28, doi:10.1080/03461238.1995.10413946.
7. János Pintz, Very large gaps between consecutive primes, Journal of Number Theory 63:2 (April 1997), pp. 286–301.
8. Leonard Adleman and Kevin McCurley, Open Problems in Number Theoretic Complexity, II. Algorithmic number theory (Ithaca, NY, 1994), 291–322, Lecture Notes in Comput. Sci., 877, Springer, Berlin, 1994.
9. Shanks, Daniel (1964), "On Maximal Gaps between Successive Primes", Mathematics of Computation, American Mathematical Society, 18 (88): 646–651, doi:10.2307/2002951, JSTOR 2002951, Zbl 0128.04203.
10. Cadwell, J. H. (1971), "Large Intervals Between Consecutive Primes", Mathematics of Computation, 25 (116): 909–913, doi:10.2307/2004355, JSTOR 2004355
11. Nicely, Thomas R. (1999), "New maximal prime gaps and first occurrences", Mathematics of Computation, 68 (227): 1311–1315, doi:10.1090/S0025-5718-99-01065-0, MR 1627813.

• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. A8. ISBN 978-0-387-20860-2. Zbl 1058.11001.
• Pintz, János (2007). "Cramér vs. Cramér. On Cramér's probabilistic model for primes". Functiones et Approximatio Commentarii Mathematici. 37: 361–376. doi:10.7169/facm/1229619660. ISSN 0208-6573. MR 2363833. Zbl 1226.11096.
• Soundararajan, K. (2007). "The distribution of prime numbers". In Granville, Andrew; Rudnick, Zeév. Equidistribution in number theory, an introduction. Proceedings of the NATO Advanced Study Institute on equidistribution in number theory, Montréal, Canada, July 11--22, 2005. NATO Science Series II: Mathematics, Physics and Chemistry. 237. Dordrecht: Springer-Verlag. pp. 59–83. ISBN 978-1-4020-5403-7. Zbl 1141.11043.

External links

• Weisstein, Eric W. "Cramér Conjecture". MathWorld.

• Weisstein, Eric W. "Cramér-Granville Conjecture". MathWorld.