Cramer–Castillon problem

Two solutions whose sides pass through $A,B,C$

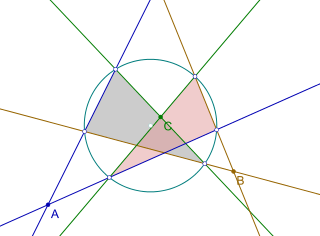
In geometry, the Cramer–Castillon problem is a problem stated by the Swiss mathematician Gabriel Cramer solved by the italian mathematician, resident in Berlin, Jean de Castillon in 1776.^[1]

The problem consists of (see the image):

Given a circle $Z$ and three points $A,B,C$ in the same plane and not on $Z$, to construct every possible triangle inscribed in $Z$ whose sides (or their elongations) pass through $A,B,C$ respectively.

Centuries before, Pappus of Alexandria had solved a special case: when the three points are collinear. But the general case had the reputation of being very difficult.^[2]

After the geometrical construction of Castillon, Lagrange found an analytic solution, easier than Castillon's. In the beginning of the 19th century, Lazare Carnot generalized it to $n$ points.^[3]

References

1. Stark, page 1.
2. Wanner, page 59.
3. Ostermann and Wanner, page 176.

Bibliography

• Dieudonné, Jean (1992). "Some problems in Classical Mathematics". Mathematics — The Music of Reason. Springer. pp. 77–101. ISBN 978-3-642-08098-2.
• Ostermann, Alexander; Wanner, Gerhard (2012). "6.9 The Cramer–Castillon problem". Geometry by Its History. Springer. pp. 175–178. ISBN 978-3-642-29162-3.
• Wanner, Gerhard (2006). "The Cramer–Castillon problem and Urquhart's `most elementary´ theorem". Elemente der Mathematik. Vol. 61 (Num. 2). pp. 58–64. doi:10.4171/EM/33. ISSN 0013-6018.

External links

• Stark, Maurice (2002). "Castillon's problem" (PDF).