Fréchet distribution

Fréchet
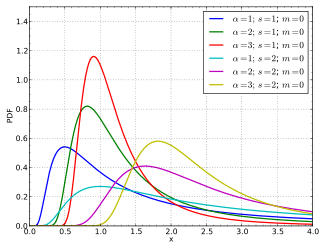
Probability density function
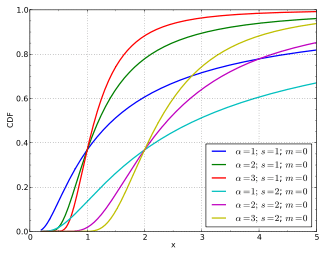
Cumulative distribution function
Parameters	$\alpha \in (0,\infty )$ shape. (Optionally, two more parameters) $s\in (0,\infty )$ scale (default: $s=1\,$ ) $m\in (-\infty ,\infty )$ location of minimum (default: $m=0\,$ )
Support	$x>m$
PDF	${\frac {\alpha }{s}}\;\left({\frac {x-m}{s}}\right)^{{-1-\alpha }}\;e^{{-({\frac {x-m}{s}})^{{-\alpha }}}}$
CDF	$e^{{-({\frac {x-m}{s}})^{{-\alpha }}}}$
Mean	${\begin{cases}\ m+s\Gamma \left(1-{\frac {1}{\alpha }}\right)&{\text{for }}\alpha >1\\\ \infty &{\text{otherwise}}\end{cases}}$
Median	$m+{\frac {s}{{\sqrt[ {\alpha }]{\log _{e}(2)}}}}$
Mode	$m+s\left({\frac {\alpha }{1+\alpha }}\right)^{{1/\alpha }}$
Variance	${\begin{cases}\ s^{2}\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\left(\Gamma \left(1-{\frac {1}{\alpha }}\right)\right)^{2}\right)&{\text{for }}\alpha >2\\\ \infty &{\text{otherwise}}\end{cases}}$
Skewness	${\begin{cases}\ {\frac {\Gamma \left(1-{\frac {3}{\alpha }}\right)-3\Gamma \left(1-{\frac {2}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+2\Gamma ^{3}\left(1-{\frac {1}{\alpha }}\right)}{{\sqrt {\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right)^{3}}}}}&{\text{for }}\alpha >3\\\ \infty &{\text{otherwise}}\end{cases}}$
Ex. kurtosis	${\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{for }}\alpha >4\\\ \infty &{\text{otherwise}}\end{cases}}$
Entropy	$1+{\frac {\gamma }{\alpha }}+\gamma +\ln \left({\frac {s}{\alpha }}\right)$ , where $\gamma$ is the Euler–Mascheroni constant.
MGF	^[1] Note: Moment $k$ exists if $\alpha >k$
CF	^[1]

The Fréchet distribution, also known as inverse Weibull distribution,^[2]^[3] is a special case of the generalized extreme value distribution. It has the cumulative distribution function

\Pr(X\leq x)=e^{{-x^{{-\alpha }}}}{\text{ if }}x>0.

where α > 0 is a shape parameter. It can be generalised to include a location parameter m (the minimum) and a scale parameter s > 0 with the cumulative distribution function

\Pr(X\leq x)=e^{{-\left({\frac {x-m}{s}}\right)^{{-\alpha }}}}{\text{ if }}x>m.

Named for Maurice Fréchet who wrote a related paper in 1927, further work was done by Fisher and Tippett in 1928 and by Gumbel in 1958.

Characteristics

The single parameter Fréchet with parameter $\alpha$ has standardized moment

\mu _{k}=\int _{0}^{\infty }x^{k}f(x)dx=\int _{0}^{\infty }t^{{-{\frac {k}{\alpha }}}}e^{{-t}}\,dt,

(with $t=x^{{-\alpha }}$ ) defined only for $k<\alpha$ :

\mu _{k}=\Gamma \left(1-{\frac {k}{\alpha }}\right)

where $\Gamma \left(z\right)$ is the Gamma function.

In particular:

For $\alpha >1$ the expectation is $E[X]=\Gamma (1-{\tfrac {1}{\alpha }})$
For $\alpha >2$ the variance is ${\text{Var}}(X)=\Gamma (1-{\tfrac {2}{\alpha }})-{\big (}\Gamma (1-{\tfrac {1}{\alpha }}){\big )}^{2}.$

The quantile $q_{y}$ of order $y$ can be expressed through the inverse of the distribution,

q_{y}=F^{{-1}}(y)=\left(-\log _{e}y\right)^{{-{\frac {1}{\alpha }}}}

In particular the median is:

q_{{1/2}}=(\log _{e}2)^{{-{\frac {1}{\alpha }}}}.

The mode of the distribution is $\left({\frac {\alpha }{\alpha +1}}\right)^{{\frac {1}{\alpha }}}.$

Especially for the 3-parameter Fréchet, the first quartile is $q_{1}=m+{\frac {s}{{\sqrt[ {\alpha }]{\log(4)}}}}$ and the third quartile $q_{3}=m+{\frac {s}{{\sqrt[ {\alpha }]{\log({\frac {4}{3}})}}}}.$

Also the quantiles for the mean and mode are:

F(mean)=\exp \left(-\Gamma ^{{-\alpha }}\left(1-{\frac {1}{\alpha }}\right)\right)

F(mode)=\exp \left(-{\frac {\alpha +1}{\alpha }}\right).

Fitted cumulative Fréchet distribution to extreme one-day rainfalls

Applications

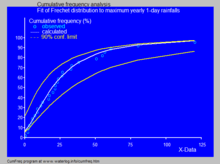
In hydrology, the Fréchet distribution is applied to extreme events such as annually maximum one-day rainfalls and river discharges.^[4] The blue picture illustrates an example of fitting the Fréchet distribution to ranked annually maximum one-day rainfalls in Oman showing also the 90% confidence belt based on the binomial distribution. The cumulative frequencies of the rainfall data are represented by plotting positions as part of the cumulative frequency analysis. However, in most hydrological applications, the distribution fitting is via the generalized extreme value distribution as this avoids imposing the assumption that the distribution does not have a lower bound (as required by the Frechet distribution).
One useful test to assess whether a multivariate distribution is asymptotically dependent or independent consists transforming the data into standard Frechet margins using transformation $Z_{i}=-1/\log F_{i}(X_{i})$ and then mapping from the cartesian to pseudo-polar coordinates $(R,W)=(Z_{1}+Z_{2},Z_{1}/(Z_{1}+Z_{2}))$ . $R>>1$ corresponds to the extreme data for which at least only one component is large while $W$ approximately 1 or 0 corresponds to only one component being extreme.

Related distributions

If $X\sim U(0,1)\,$ (Uniform distribution (continuous)) then $m+s(-\log(X))^{{-1/\alpha }}\sim {\textrm {Frechet}}(\alpha ,s,m)\,$
If $X\sim {\textrm {Frechet}}(\alpha ,s,m)\,$ then $kX+b\sim {\textrm {Frechet}}(\alpha ,ks,km+b)\,$
If $X_{i}\sim {\textrm {Frechet}}(\alpha ,s,m)\,$ and $Y=\max\{\,X_{1},\ldots ,X_{n}\,\}\,$ then $Y\sim {\textrm {Frechet}}(\alpha ,n^{{{\tfrac {1}{\alpha }}}}s,m)\,$
The cumulative distribution function of the Frechet distribution solves the maximum stability postulate equation
If $X\sim {\textrm {Frechet}}(\alpha ,s,m=0)\,$ then its reciprocal is Weibull-distributed: $X^{{-1}}\sim {\textrm {Weibull}}(k=\alpha ,\lambda =s^{{-1}})\,$

Properties

The Frechet distribution is a max stable distribution
The negative of a random variable having a Frechet distribution is a min stable distribution

References

1 2 Muraleedharan. G, C. Guedes Soares and Cláudia Lucas (2011). "Characteristic and Moment Generating Functions of Generalised Extreme Value Distribution (GEV)". In Linda. L. Wright (Ed.), Sea Level Rise, Coastal Engineering, Shorelines and Tides, Chapter 14, pp. 269–276. Nova Science Publishers. ISBN 978-1-61728-655-1
↑ Khan M.S.; Pasha G.R.; Pasha A.H. (February 2008). "Theoretical Analysis of Inverse Weibull Distribution" (PDF). WSEAS TRANSACTIONS on MATHEMATICS. 7 (2). pp. 30–38.
↑ de Gusmão, FelipeR.S. and Ortega, EdwinM.M. and Cordeiro, GaussM. (2011). "The generalized inverse Weibull distribution". Statistical Papers. 52 (3). Springer-Verlag. pp. 591–619. doi:10.1007/s00362-009-0271-3. ISSN 0932-5026.
↑ Coles, Stuart (2001). An Introduction to Statistical Modeling of Extreme Values,. Springer-Verlag. ISBN 1-85233-459-2.

Publications

Fréchet, M., (1927). "Sur la loi de probabilité de l'écart maximum." Ann. Soc. Polon. Math. 6, 93.
Fisher, R.A., Tippett, L.H.C., (1928). "Limiting forms of the frequency distribution of the largest and smallest member of a sample." Proc. Cambridge Philosophical Society 24:180–190.
Gumbel, E.J. (1958). "Statistics of Extremes." Columbia University Press, New York.
Kotz, S.; Nadarajah, S. (2000) Extreme value distributions: theory and applications, World Scientific. ISBN 1-86094-224-5

External links

Probability distributions

List

Discrete univariate with finite support	Benford Bernoulli beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support	beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval	arcsine ARGUS Balding–Nichols Bates beta beta rectangular Irwin–Hall Kumaraswamy logit-normal noncentral beta raised cosine reciprocal triangular U-quadratic uniform Wigner semicircle

Continuous univariate supported on a semi-infinite interval	Benini Benktander 1st kind Benktander 2nd kind beta prime Burr chi-squared chi Dagum Davis exponential-logarithmic Erlang exponential F folded normal Flory–Schulz Fréchet gamma gamma/Gompertz generalized inverse Gaussian Gompertz half-logistic half-normal Hotelling's T-squared hyper-Erlang hyperexponential hypoexponential inverse chi-squared scaled inverse chi-squared inverse Gaussian inverse gamma Kolmogorov Lévy log-Cauchy log-Laplace log-logistic log-normal Lomax matrix-exponential Maxwell–Boltzmann Maxwell–Jüttner Mittag-Leffler Nakagami noncentral chi-squared Pareto phase-type poly-Weibull Rayleigh relativistic Breit–Wigner Rice shifted Gompertz truncated normal type-2 Gumbel Weibull Discrete Weibull Wilks's lambda

Continuous univariate supported on the whole real line	Cauchy exponential power Fisher's z Gaussian q generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson's S_U Landau Laplace asymmetric Laplace logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt

Continuous univariate with support whose type varies	generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential q-Weibull shifted log-logistic

Mixed continuous-discrete univariate	rectified Gaussian

Multivariate (joint)	Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet generalized Dirichlet multivariate normal multivariate stable multivariate t normal-inverse-gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional	Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular	Degenerate Dirac delta function Singular Cantor

Families	Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia - version of the 10/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.