Gamma/Gompertz distribution
|
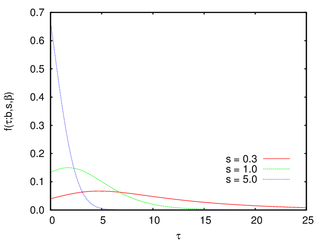
Probability density function
| |
|
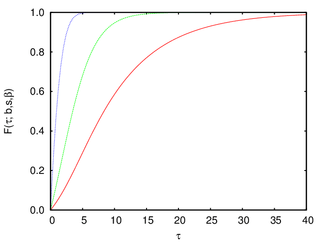
Cumulative distribution function
| |
| Parameters | |
|---|---|
| Support | |
| CDF |
|
| Mean |
|
| Median | |
| Mode | |
| Variance |
|
| MGF |
|
In probability and statistics, the Gamma/Gompertz distribution is a continuous probability distribution. It has been used as an aggregate-level model of customer lifetime and a model of mortality risks.
Specification
Probability density function
The probability density function of the Gamma/Gompertz distribution is:
where is the scale parameter and are the shape parameters of the Gamma/Gompertz distribution.
Cumulative distribution function
The cumulative distribution function of the Gamma/Gompertz distribution is:
Moment generating function
The moment generating function is given by:
where is a Hypergeometric function.
Properties
The Gamma/Gompertz distribution is a flexible distribution that can be skewed to the right or to the left.
Related distributions
- When β = 1, this reduces to an Exponential distribution with parameter sb.
- The gamma distribution is a natural conjugate prior to a Gompertz likelihood with known, scale parameter [1]
- When the shape parameter of a Gompertz distribution varies according to a gamma distribution with shape parameter and scale parameter (mean = ), the distribution of is Gamma/Gompertz.[1]
See also
Notes
References
- Bemmaor, Albert C.; Glady, Nicolas (2012). "Modeling Purchasing Behavior With Sudden 'Death': A Flexible Customer Lifetime Model". Management Science. 58 (5): 1012–1021. doi:10.1287/mnsc.1110.1461.
- Bemmaor, Albert C.; Glady, Nicolas (2011). "Implementing the Gamma/Gompertz/NBD Model in MATLAB" (PDF). Cergy-Pontoise: ESSEC Business School.
- Gompertz, B. (1825). "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies". Philosophical Transactions of the Royal Society of London. 115: 513–583. doi:10.1098/rstl.1825.0026. JSTOR 107756.
- Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). "Continuous Univariate Distributions". 2 (2nd ed.). New York: John Wiley & Sons: 25–26. ISBN 0-471-58494-0.
- Manton, K. G.; Stallard, E.; Vaupel, J. W. (1986). "Alternative Models for the Heterogeneity of Mortality Risks Among the Aged". Journal of the American Statistical Association. 81: 635–644. doi:10.1080/01621459.1986.10478316.
This article is issued from Wikipedia - version of the 6/16/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.