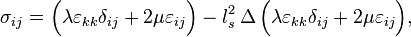GRADELA

GRADELA is a simple gradient elasticity model involving one internal length in addition to the two Lamé parameters. It allows to eliminate elastic singularities and discontinuities and to interpret elastic size effects. This model has been suggested by Elias C. Aifantis. The main advantage of GRADELA over Mindlin's elasticity models (which contains five extra constants) is the fact that solutions of boundary value problems can be found in terms of corresponding solutions of classical elasticity by operator splitting method.

In 1992-1993 it has been suggested by Elias C. Aifantis a generalization of the linear elastic constitutive relations by the gradient modification that contains the Laplacian in the form

$\sigma_{ij} = \Bigl( \lambda \varepsilon_{kk} \delta_{ij} + 2 \mu \varepsilon_{ij} \Bigr) - l^2_s \, \Delta \, \Bigl( \lambda \varepsilon_{kk} \delta_{ij} + 2 \mu \varepsilon_{ij} \Bigr) ,$

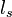where $l_s$ is the scale parameter.

References

• E. C. Aifantis, "On the role of gradients in the localization of deformation and fracture" International Journal of Engineering Science Volume 30, Issue 10, October 1992, Pages 1279–1299
• E. C. Aifantis, "On non-singular GRADELA crack fields" Theor. Appl. Mech. Lett. 2014, Vol. 4 Issue (5): 5-051005 DOI: 10.1063/2.1405105
• E. C. Aifantis, "On the gradient approach – Relation to Eringen’s nonlocal theory" International Journal of Engineering Science Volume 49, Issue 12, December 2011, Pages 1367–1377
• C. Q. Ru, E. C.Aifantis, "A simple approach to solve boundary value problems in gradient elasticity. Acta Mechanica, 1993, Volume 101, Issue 1-4, pp 59-68.

See also

• Linear elasticity
• Mindlin–Reissner plate theory
• Gradela fish