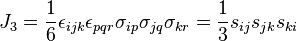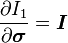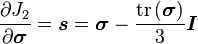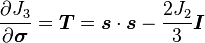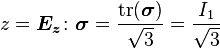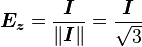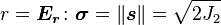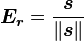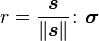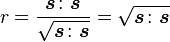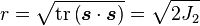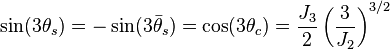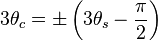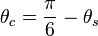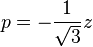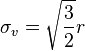Lode Coordinates
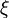 ,
, 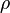 ,
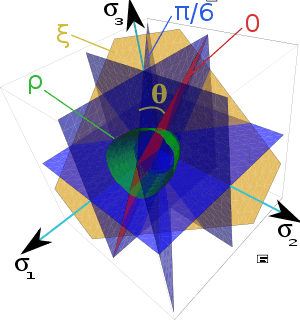
, 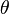 are constant. Plotted in principal stress space. The red plane represents a meridional plane and the yellow plane represents an octahedral plane.
are constant. Plotted in principal stress space. The red plane represents a meridional plane and the yellow plane represents an octahedral plane.Lode coordinates 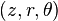 or Haigh-Westergaard coordinates
or Haigh-Westergaard coordinates 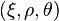 .[1] are a set of tensor invariants that span the space of real, symmetric, second-order, 3-dimensional tensors and are isomorphic with respect to principal stress space. This right-handed orthogonal coordinate system is named in honor of the German scientist Dr. Walter Lode because of his seminal paper written in 1926 describing the effect of the middle principal stress on metal plasticity.[2] Other examples of sets of tensor invariants are the set of principal stresses
.[1] are a set of tensor invariants that span the space of real, symmetric, second-order, 3-dimensional tensors and are isomorphic with respect to principal stress space. This right-handed orthogonal coordinate system is named in honor of the German scientist Dr. Walter Lode because of his seminal paper written in 1926 describing the effect of the middle principal stress on metal plasticity.[2] Other examples of sets of tensor invariants are the set of principal stresses 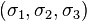 or the set of mechanics invariants
or the set of mechanics invariants 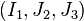 . The Lode coordinate system can be described as a cylindrical coordinate system within principal stress space with a coincident origin and the z-axis parallel to the vector
. The Lode coordinate system can be described as a cylindrical coordinate system within principal stress space with a coincident origin and the z-axis parallel to the vector 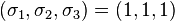 .
.
Mechanics Invariants
The Lode coordinates are most easily computed using the mechanics invariants. These invariants are a mixture of the invariants of the Cauchy stress tensor, 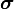 , and the stress deviator,
, and the stress deviator,  , and are given by[3]
, and are given by[3]
which can be written equivalently in Einstein notation
where  is the Levi-Civita symbol (or permutation symbol) and the last two forms for
is the Levi-Civita symbol (or permutation symbol) and the last two forms for 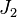 are equivalent because
are equivalent because  is symmetric (
is symmetric (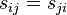 ).
).
The gradients of these invariants[4] can be calculated by
where 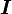 is the 3x3 identity matrix and
is the 3x3 identity matrix and 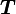 is called the Hill tensor.
is called the Hill tensor.
Axial Coordinate 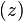
The 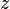 -coordinate is found by calculating the magnitude of the orthogonal projection of the stress state onto the hydrostatic axis.
-coordinate is found by calculating the magnitude of the orthogonal projection of the stress state onto the hydrostatic axis.
where
is the unit normal in the direction of the hydrostatic axis.
Radial Coordinate 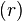
The  -coordinate is found by calculating the magnitude of the stress deviator (the orthogonal projection of the stress state into the deviatoric plane).
-coordinate is found by calculating the magnitude of the stress deviator (the orthogonal projection of the stress state into the deviatoric plane).
where
Derivation The relation that 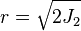 can be found by expanding the relation
can be found by expanding the relation
and writing
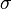 in terms of the isotropic and deviatoric parts while expanding the magnitude of
in terms of the isotropic and deviatoric parts while expanding the magnitude of 
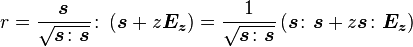 .
.
Because
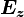 is isotropic and
is isotropic and  is deviatoric, their product is zero. Which leaves us with
is deviatoric, their product is zero. Which leaves us withApplying the identity
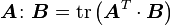 and using the definition of
and using the definition of 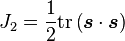
is a unit tensor in the direction of the radial component.
Lode Angle - Angular Coordinate 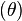
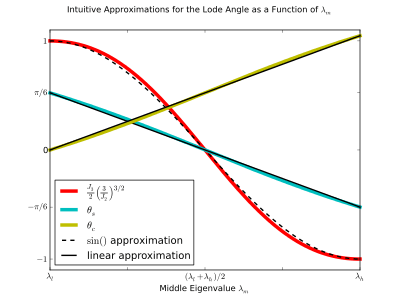
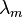 with respect to the low and high principal stresses.
with respect to the low and high principal stresses.The Lode angle can be considered, rather loosely, a measure of loading type. The Lode angle varies with respect to the middle eigenvalue of the stress. There are many definitions of Lode angle that each utilize different trigonometric functions: the positive sine,[5] negative sine,[6] and positive cosine[7] (here denoted 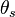 ,
, 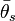 , and
, and 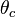 , respectively)
, respectively)
and are related by
Derivation The relation between 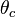 and
and 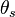 can be shown by applying a trigonometric identity relating sine and cosine by a shift
can be shown by applying a trigonometric identity relating sine and cosine by a shift
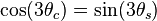
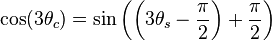
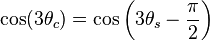 .
.
Because cosine is an even function and the range of the inverse cosine is usually
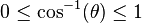 we take the negative possible value for the
we take the negative possible value for the 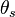 term, thus ensuring that
term, thus ensuring that 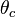 is positive.
is positive.
These definitions are all defined for a range of 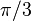 .
.
Stress State 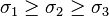 |
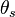 |
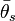 |
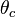 | |
|---|---|---|---|---|
| range | 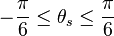 | 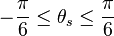 | 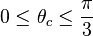 | |
| Triaxial Compression (TXC) | 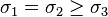 | 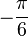 | 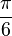 | 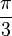 |
| Shear (SHR) | 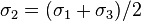 |  |  | 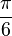 |
| Triaxial Extension (TXE) | 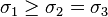 | 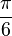 | 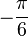 |  |
The unit normal in the angular direction which completes the orthonormal basis can be calculated for 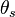 [8] and
[8] and 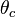 [9] using
[9] using
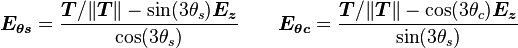 .
.
Meridional Profile
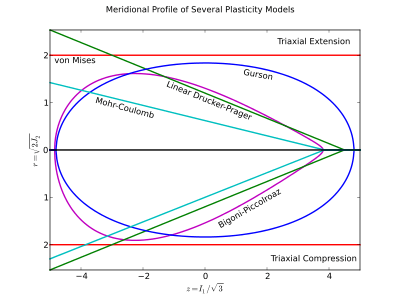
The meridional profile is a 2D plot of  holding
holding  constant and is sometimes plotted using scalar multiples of
constant and is sometimes plotted using scalar multiples of 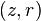 . It is commonly used to demonstrate the pressure dependence of a yield surface or the pressure-shear trajectory of a stress path. Because
. It is commonly used to demonstrate the pressure dependence of a yield surface or the pressure-shear trajectory of a stress path. Because  is non-negative the plot usually omits the negative portion of the
is non-negative the plot usually omits the negative portion of the  -axis, but can be included to illustrate effects at opposing Lode angles (usually triaxial extension and triaxial compression).
-axis, but can be included to illustrate effects at opposing Lode angles (usually triaxial extension and triaxial compression).
One of the benefits of plotting the meridional profile with 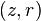 is that it is a geometrically accurate depiction of the yield surface.[8] If a non-isomorphic pair is used for the meridional profile then the normal to the yield surface will not appear normal in the meridional profile. Any pair of coordinates that differ from
is that it is a geometrically accurate depiction of the yield surface.[8] If a non-isomorphic pair is used for the meridional profile then the normal to the yield surface will not appear normal in the meridional profile. Any pair of coordinates that differ from 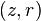 by constant multiples of equal absolute value are also isomorphic with respect to principal stress space. As an example, pressure
by constant multiples of equal absolute value are also isomorphic with respect to principal stress space. As an example, pressure 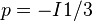 and the Von Mises stress
and the Von Mises stress 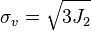 are not an isomorphic coordinate pair and, therefore, distort the yield surface because
are not an isomorphic coordinate pair and, therefore, distort the yield surface because
and, finally, 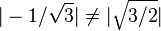 .
.
Octahedral Profile
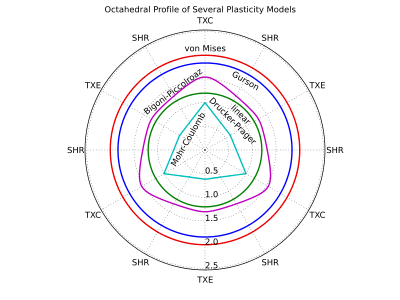
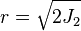 .
.The octahedral profile is a 2D plot of 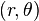 holding
holding 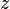 constant. Plotting the yield surface in the octahedral plane demonstrates the level of Lode angle dependence. The octahedral plane is sometimes referred to as the 'pi plane'[10] or 'deviatoric plane'.[11]
constant. Plotting the yield surface in the octahedral plane demonstrates the level of Lode angle dependence. The octahedral plane is sometimes referred to as the 'pi plane'[10] or 'deviatoric plane'.[11]
The octahedral profile is not necessarily constant for different values of pressure with the notable exceptions of the von Mises yield criterion and the Tresca yield criterion which are constant for all values of pressure.
A Note on Terminology
The term Haigh-Westergaard space is ambiguously used in the literature to mean both the Cartesian principal stress space[12][13] and the cylindrical Lode coordinate space[14][15]
See also
- Yield (engineering)
- Plasticity (physics)
- Stress
- Henri Tresca
- von Mises stress
- Mohr–Coulomb theory
- Strain
- Strain tensor
- Stress–energy tensor
- Stress concentration
- 3-D elasticity
References
- ↑ Menetrey, P.H., Willam, K.J., 1995, Triaxial Failure Criterion for Concrete and Its Generalization, ACI Structural Journal
- ↑ Lode, W. (1926). Versuche über den Einfuss der mittleren Hauptspannung auf das Fliessen der Metalle Eisen Kupfer und Nickel. Zeitung Phys., vol. 36, pp. 913–939.
- ↑ Asaro, R.J., Lubarda, V.A., 2006, Mechanics of Solids and Materials, Cambridge University Press
- ↑ Brannon, R.M., 2009, KAYENTA: Theory and User's Guide, Sandia National Laboratories, Albuquerque, New Mexico.
- ↑ Chakrabarty, J., 2006, Theory of Plasticity: Third edition, Elsevier, Amsterdam.
- ↑ de Souza Neto, E.A., Peric, D., Owen, D.R.J., 2008, Computational Methods for Plasticity, Wiley
- ↑ Han, D.J., Chen, W.F., 1985, A Nonuniform Hardening Plasticity Model for Concrete Materials, Mechanics of Materials
- 1 2 Brannon, R.M., 2007, Elements of Phenomenological Plasticity: Geometrical Insight, Computational Algorithms, and Topics in Shock Physics, Shock Wave Science and Technology Reference Library: Solids I, Springer-New York
- ↑ Bigoni, D., Piccolroaz, A., 2004, Yield criteria for quasibrittle and frictional materials, Int. J. Solids Struct.
- ↑ Lubliner, J., 1990, Plasticity Theory, Pearson Education
- ↑ Chaboche, J.L., 2008, A review of some plasticity and viscoplasticity theories, Int. J. Plasticity
- ↑ Mouazen, A.M., Nemenyi, M., 1998, A review of the finite element modelling techniques of soil tillage, Mathematics and Computers in Simulation
- ↑ Keryvin, V., 2008, Indentation as a probe for pressure sensitivity of metallic glasses, J. Phys.: Condens. Matter
- ↑ Cervenka, J., Papanikolaou, V.K., 2008, Three dimensional combined fracture-plastic material model for concrete, Int. J. of Plasticity
- ↑ Piccolroaz, A., Bigoni, D., 2009, Yield criteria for quasibrittle and frictional materials: A generalization to surfaces with corners, Int. J. of Solids and Struc.
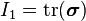
![J_2 = \frac{1}{2}\left[\text{tr}(\boldsymbol{\sigma}^2) - \frac{1}{3}\text{tr}(\boldsymbol{\sigma})^2\right] = \frac{1}{2}\mathrm{tr}\left(\boldsymbol{s}\cdot\boldsymbol{s}\right) = \frac{1}{2}\lVert \boldsymbol{s} \rVert^2](../I/m/77a29d4b3f3c9d14b283ca6d54241065.png)
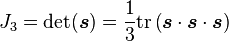
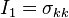
![J_2 = \frac{1}{2}\left[\text{tr}(\boldsymbol{\sigma}^2) - \frac{1}{3}\text{tr}(\boldsymbol{\sigma})^2\right] = \frac{1}{2}s_{ij}s_{ji} = \frac{1}{2}s_{ij}s_{ij}](../I/m/8ee1fad1350ea8e3b284f2d85b0de3c4.png)