Quadratic differential
In mathematics, a quadratic differential on a Riemann surface is a section of the symmetric square of the holomorphic cotangent bundle. If the section is holomorphic, then the quadratic differential is said to be holomorphic. The vector space of holomorphic quadratic differentials on a Riemann surface has a natural interpretation as the cotangent space to the Riemann moduli space or Teichmueller space.
Local form
Each quadratic differential on a domain 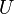 in the complex plane may be written as
in the complex plane may be written as
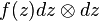 where
where 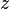 is the complex variable and
is the complex variable and
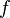 is a complex valued function on
is a complex valued function on 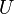 .
Such a `local' quadratic differential is holomorphic if and only if
.
Such a `local' quadratic differential is holomorphic if and only if 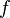 is holomorphic.
Given a chart
is holomorphic.
Given a chart 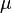 for a general Riemann surface
for a general Riemann surface 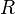 and a quadratic differential
and a quadratic differential 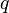 on
on 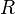 , the pull-back
, the pull-back
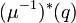 defines a quadratic differential on a domain in the complex plane.
defines a quadratic differential on a domain in the complex plane.
Relation to abelian differentials
If 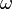 is an abelian differential on a Riemann surface,
then
is an abelian differential on a Riemann surface,
then 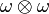 is a quadratic differential.
is a quadratic differential.
Singular Euclidean structure
A holomorphic quadratic differential 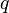 determines a Riemannian metric
determines a Riemannian metric  on
the complement of its zeroes. If
on
the complement of its zeroes. If 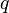 is defined on a domain in the complex plane
and
is defined on a domain in the complex plane
and 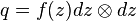 , then the associated Riemannian metric is
, then the associated Riemannian metric is
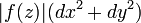 where
where 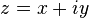 .
Since
.
Since 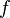 is holomorphic, the curvature of this metric is zero. Thus,
a holomorphic quadratic differential defines a flat metric on the complement of the
set of
is holomorphic, the curvature of this metric is zero. Thus,
a holomorphic quadratic differential defines a flat metric on the complement of the
set of 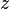 such that
such that 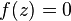 .
.
References
- Kurt Strebel, Quadratic differentials. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 5. Springer-Verlag, Berlin, 1984. xii+184 pp. ISBN 3-540-13035-7
- Y. Imayoshi and M. Taniguchi, M. An introduction to Teichmüller spaces. Translated and revised from the Japanese version by the authors. Springer-Verlag, Tokyo, 1992. xiv+279 pp. ISBN 4-431-70088-9