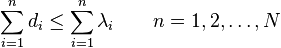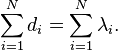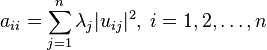Schur–Horn theorem
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
Statement
Theorem. Let 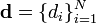 and
and 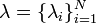 be vectors in
be vectors in 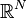 such that their entries are in non-increasing order. There is a Hermitian matrix with diagonal values
such that their entries are in non-increasing order. There is a Hermitian matrix with diagonal values 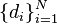 and eigenvalues
and eigenvalues 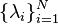 if and only if
if and only if
and
Polyhedral geometry perspective
Permutation polytope generated by a vector
The permutation polytope generated by  denoted by
denoted by 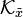 is defined as the convex hull of the set
is defined as the convex hull of the set 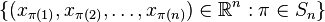 . Here
. Here 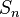 denotes the symmetric group on
denotes the symmetric group on 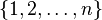 . The following lemma characterizes the permutation polytope of a vector in
. The following lemma characterizes the permutation polytope of a vector in 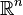 .
.
Lemma.[1][2] If 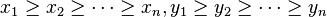 , and
, and 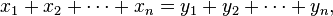 then the following are equivalent :
then the following are equivalent :
(i) 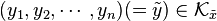 .
.
(ii) 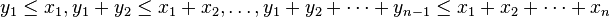
(iii) There are points 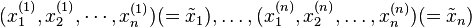 in
in 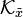 such that
such that 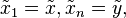 and
and 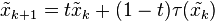 for each
for each 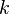 in
in 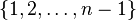 , some transposition
, some transposition 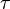 in
in 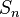 , and some
, and some 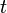 in
in ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) , depending on
, depending on 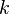 .
.
Reformulation of Schur–Horn theorem
In view of the equivalence of (i) and (ii) in the lemma mentioned above, one may reformulate the theorem in the following manner.
Theorem. Let 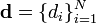 and
and 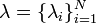 be real vectors. There is a Hermitian matrix with diagonal entries
be real vectors. There is a Hermitian matrix with diagonal entries 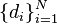 and eigenvalues
and eigenvalues 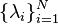 if and only if the vector
if and only if the vector 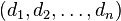 is in the permutation polytope generated by
is in the permutation polytope generated by 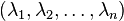 .
.
Note that in this formulation, one does not need to impose any ordering on the entries of the vectors 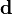 and
and 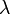 .
.
Proof of the Schur–Horn theorem
Let 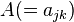 be a
be a 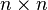 Hermitian matrix with eigenvalues
Hermitian matrix with eigenvalues 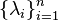 , counted with multiplicity. Denote the diagonal of
, counted with multiplicity. Denote the diagonal of 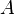 by
by 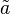 , thought of as a vector in
, thought of as a vector in 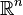 , and the vector
, and the vector 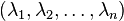 by
by 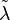 . Let
. Let 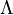 be the diagonal matrix having
be the diagonal matrix having 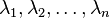 on its diagonal.
on its diagonal.
(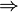 )
) 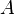 may be written in the form
may be written in the form 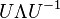 , where
, where 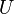 is a unitary matrix. Then
is a unitary matrix. Then
Let 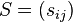 be the matrix defined by
be the matrix defined by 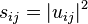 . Since
. Since 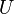 is a unitary matrix,
is a unitary matrix, 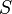 is a doubly stochastic matrix and we have
is a doubly stochastic matrix and we have 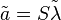 . By the Birkhoff–von Neumann theorem,
. By the Birkhoff–von Neumann theorem, 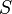 can be written as a convex combination of permutation matrices. Thus
can be written as a convex combination of permutation matrices. Thus 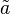 is in the permutation polytope generated by
is in the permutation polytope generated by 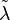 . This proves Schur's theorem.
. This proves Schur's theorem.
( ) If
) If 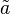 occurs as the diagonal of a Hermitian matrix with eigenvalues
occurs as the diagonal of a Hermitian matrix with eigenvalues 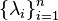 , then
, then 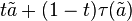 also occurs as the diagonal of some Hermitian matrix with the same set of eigenvalues, for any transposition
also occurs as the diagonal of some Hermitian matrix with the same set of eigenvalues, for any transposition 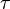 in
in 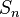 . One may prove that in the following manner.
. One may prove that in the following manner.
Let 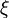 be a complex number of modulus
be a complex number of modulus 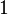 such that
such that 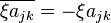 and
and 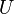 be a unitary matrix with
be a unitary matrix with  in the
in the 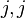 and
and 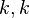 entries, respectively,
entries, respectively, 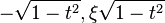 at the
at the 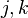 and
and 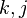 entries, respectively,
entries, respectively, 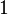 at all diagonal entries other than
at all diagonal entries other than 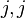 and
and 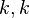 , and
, and  at all other entries. Then
at all other entries. Then 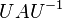 has
has 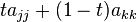 at the
at the  entry,
entry, 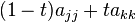 at the
at the 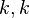 entry, and
entry, and 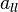 at the
at the 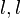 entry where
entry where 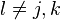 . Let
. Let 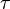 be the transposition of
be the transposition of 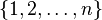 that interchanges
that interchanges 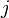 and
and 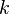 .
.
Then the diagonal of 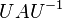 is
is 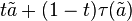 .
.
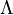 is a Hermitian matrix with eigenvalues
is a Hermitian matrix with eigenvalues 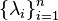 . Using the equivalence of (i) and (iii) in the lemma mentioned above, we see that any vector in the permutation polytope generated by
. Using the equivalence of (i) and (iii) in the lemma mentioned above, we see that any vector in the permutation polytope generated by 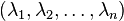 , occurs as the diagonal of a Hermitian matrix with the prescribed eigenvalues. This proves Horn's theorem.
, occurs as the diagonal of a Hermitian matrix with the prescribed eigenvalues. This proves Horn's theorem.
Symplectic geometry perspective
The Schur–Horn theorem may be viewed as a corollary of the Atiyah–Guillemin–Sternberg convexity theorem in the following manner. Let 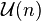 denote the group of
denote the group of 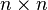 unitary matrices. Its Lie algebra, denoted by
unitary matrices. Its Lie algebra, denoted by 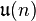 , is the set of skew-Hermitian matrices. One may identify the dual space
, is the set of skew-Hermitian matrices. One may identify the dual space 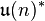 with the set of Hermitian matrices
with the set of Hermitian matrices 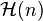 via the linear isomorphism
via the linear isomorphism 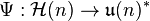 defined by
defined by 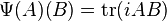 for
for 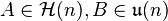 . The unitary group
. The unitary group 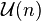 acts on
acts on 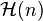 by conjugation and acts on
by conjugation and acts on 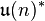 by the coadjoint action. Under these actions,
by the coadjoint action. Under these actions, 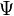 is an
is an 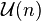 -equivariant map i.e. for every
-equivariant map i.e. for every 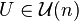 the following diagram commutes,
the following diagram commutes,
-equivariance_of_isomorphism.png)
Let 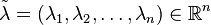 and
and 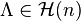 denote the diagonal matrix with entries given by
denote the diagonal matrix with entries given by 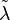 . Let
. Let 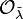 denote the orbit of
denote the orbit of 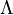 under the
under the 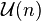 -action i.e. conjugation. Under the
-action i.e. conjugation. Under the 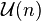 -equivariant isomorphism
-equivariant isomorphism 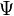 , the symplectic structure on the corresponding coadjoint orbit may be brought onto
, the symplectic structure on the corresponding coadjoint orbit may be brought onto 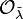 . Thus
. Thus 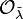 is a Hamiltonian
is a Hamiltonian 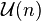 -manifold.
-manifold.
Let 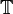 denote the Cartan subgroup of
denote the Cartan subgroup of 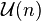 which consists of diagonal complex matrices with diagonal entries of modulus
which consists of diagonal complex matrices with diagonal entries of modulus 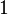 . The Lie algebra
. The Lie algebra 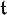 of
of 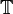 consists of diagonal skew-Hermitian matrices and the dual space
consists of diagonal skew-Hermitian matrices and the dual space 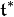 consists of diagonal Hermitian matrices, under the isomorphism
consists of diagonal Hermitian matrices, under the isomorphism 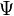 . In other words,
. In other words, 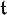 consists of diagonal matrices with purely imaginary entries and
consists of diagonal matrices with purely imaginary entries and 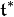 consists of diagonal matrices with real entries. The inclusion map
consists of diagonal matrices with real entries. The inclusion map 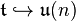 induces a map
induces a map 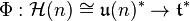 , which projects a matrix
, which projects a matrix 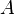 to the diagonal matrix with the same diagonal entries as
to the diagonal matrix with the same diagonal entries as 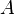 . The set
. The set 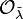 is a Hamiltonian
is a Hamiltonian 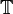 -manifold, and the restriction of
-manifold, and the restriction of 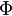 to this set is a moment map for this action.
to this set is a moment map for this action.
By the Atiyah–Guillemin–Sternberg theorem, 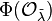 is a convex polytope. A matrix
is a convex polytope. A matrix 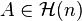 is fixed under conjugation by every element of
is fixed under conjugation by every element of 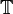 if and only if
if and only if 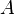 is diagonal. The only diagonal matrices in
is diagonal. The only diagonal matrices in 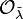 are the ones with diagonal entries
are the ones with diagonal entries 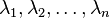 in some order. Thus, these matrices generate the convex polytope
in some order. Thus, these matrices generate the convex polytope 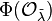 . This is exactly the statement of the Schur–Horn theorem.
. This is exactly the statement of the Schur–Horn theorem.
Notes
- ↑ Kadison, R. V., Lemma 5, The Pythagorean Theorem: I. The finite case, Proc. Natl. Acad. Sci. USA, vol. 99 no. 7 (2002):4178–4184 (electronic)
- ↑ Kadison, R. V.; Pedersen, G. K., Lemma 13, Means and Convex Combinations of Unitary Operators, Math. Scand. 57 (1985),249–266
References
- Schur, Issai, Über eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie, Sitzungsber. Berl. Math. Ges. 22 (1923), 9–20.
- Horn, Alfred, Doubly stochastic matrices and the diagonal of a rotation matrix, American Journal of Mathematics 76 (1954), 620–630.
- Kadison, R. V.; Pedersen, G. K., Means and Convex Combinations of Unitary Operators, Math. Scand. 57 (1985),249–266.
- Kadison, R. V., The Pythagorean Theorem: I. The finite case, Proc. Natl. Acad. Sci. USA, vol. 99 no. 7 (2002):4178–4184 (electronic)