Square packing in a square
Square packing in a square is a packing problem where the objective is to determine how many squares of side 1 (unit squares) can be packed into a square of side a. Obviously, if a is an integer, the answer is a2, but the precise, or even asymptotic, amount of wasted space for non-integer a is an open question.
Proven minimum solutions:[1]
| Number of squares | Square size |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 2 |
| 4 | 2 |
| 5 | 2.707 (2 + 2 −1/2) 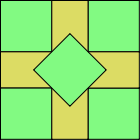 |
| 6 | 3 |
| 7 | 3  |
| 8 | 3 |
| 9 | 3 |
| 10 | 3.707 (3 + 2 −1/2) 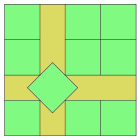 |
Other results:
- If it is possible to pack n2 − 2 unit squares in a square of side a, then a ≥ n.[2]
- The naive approach in which all squares are parallel to the coordinate axes, and are placed touching edge-to-edge, leaves wasted space of less than 2a + 1.[1]
- The wasted space of an optimal solution is asymptotically o(a7/11).[3]
- All solutions must waste space at least Ω(a1/2) for some values of a.[4]
- 11 unit squares cannot be packed in a square of side less than .[5]
See also
References
- 1 2 Friedman, Erich (1998), "Packing unit squares in squares: a survey and new results", Electronic Journal of Combinatorics, 5, Dynamic Survey 7, 24 pp., MR 1668055.
- ↑ Kearney, Michael J.; Shiu, Peter (2002), "Efficient packing of unit squares in a square", Electronic Journal of Combinatorics, 9 (1), Research Paper 14, 14 pp., MR 1912796.
- ↑ Erdős, P.; Graham, R. L. (1975), "On packing squares with equal squares" (PDF), Journal of Combinatorial Theory, Series A, 19: 119–123, doi:10.1016/0097-3165(75)90099-0, MR 0370368.
- ↑ Roth, K. F.; Vaughan, R. C. (1978), "Inefficiency in packing squares with unit squares", Journal of Combinatorial Theory, Series A, 24 (2): 170–186, doi:10.1016/0097-3165(78)90005-5, MR 0487806.
- ↑ Stromquist, Walter (2003), "Packing 10 or 11 unit squares in a square", Electronic Journal of Combinatorics, 10, Research paper 8, 11pp., MR 2386538.
This article is issued from Wikipedia - version of the 10/10/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.