Circle packing in a square

Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square; or, equivalently, to arrange n points in a unit square for the greatest minimal separation, d_n, between points.^[1] To convert between these two formulations of the problem, the square side for unit circles will be $L=2+{\frac {2}{d_{n}}}$.

Solutions (not necessarily optimal) have been computed for every N≤10,000.^[2] Solutions up to N=20 are shown below.:^[2]

Number of circles	Square size (side length)	dn[1]	Number density	Figure
1	2	∞	0.25
2	$2+{\sqrt {2}}$ ≈ 3.414...	${\sqrt {2}}$ ≈ 1.414...	0.172...
3	$2+{\frac {{\sqrt {2}}}{2}}+{\frac {{\sqrt {6}}}{2}}$ ≈ 3.931...	${\sqrt {6}}-{\sqrt {2}}$ ≈ 1.035...	0.194...
4	4	1	0.25
5	$2+2{\sqrt {2}}$ ≈ 4.828...	${\frac {1}{2}}{\sqrt {2}}$ ≈ 0.707...	0.215...
6	$2+{\frac {12}{{\sqrt {13}}}}$ ≈ 5.328...	${\frac {1}{6}}{\sqrt {13}}$ ≈ 0.601...	0.211...
7	$4+{\sqrt {3}}$ ≈ 5.732...	$4-2{\sqrt {3}}$ ≈ 0.536...	0.213...
8	$2+{\sqrt {2}}+{\sqrt {6}}$ ≈ 5.863...	${\frac {1}{2}}({\sqrt {6}}-{\sqrt {2}})$ ≈ 0.518...	0.233...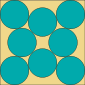
9	6	0.5	0.25
10	6.747...	0.421...	0.220...
11	7.022...	0.398...	0.223...
12	$2+15{\sqrt {{\frac {2}{17}}}}$ ≈ 7.144...	0.389...	0.235...
13	7.463...	0.366...	0.233...
14	$6+{\sqrt {3}}$ ≈ 7.732...	0.348...	0.226...
15	$4+{\sqrt {2}}+{\sqrt {6}}$ ≈ 7.863...	0.341...	0.243...
16	8	0.333...	0.25
17	8.532...	0.306...	0.234...
18	$2+{\frac {24}{{\sqrt {13}}}}$ ≈ 8.656...	0.300...	0.240...
19	8.907...	0.290...	0.240...
20	${\frac {130}{17}}+{\frac {16}{17}}{\sqrt {2}}$ ≈ 8.978...	0.287...	0.248...

References

1. Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Unsolved Problems in Geometry. New York: Springer-Verlag. pp. 108–110. ISBN 0-387-97506-3.
2. Eckard Specht (20 May 2010). "The best known packings of equal circles in a square". Retrieved 25 May 2010.