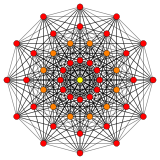
Cantic 7-cube

Truncated 7-demicube
Cantic 7-cube

D7 Coxeter plane projection
Typeuniform 7-polytope
Schläfli symbol t{3,34,1}
h2{4,3,3,3,3,3}
Coxeter diagram
6-faces142
5-faces1428
4-faces5656
Cells11760
Faces13440
Edges7392
Vertices1344
Coxeter groupsD7, [34,1,1]
Propertiesconvex

In seven-dimensional geometry, a cantic 7-cube or truncated 7-demicube as a uniform 7-polytope, being a truncation of the 7-demicube.

A uniform 7-polytope is vertex-transitive and constructed from uniform 6-polytope facets, and can be represented a coxeter diagram with ringed nodes representing active mirrors. A demihypercube is an alternation of a hypercube.

Its 3-dimensional analogue would be a truncated tetrahedron (truncated 3-demicube), and Coxeter diagram or as a cantic cube.

Alternate names

Cartesian coordinates

The Cartesian coordinates for the 1344 vertices of a truncated 7-demicube centered at the origin and edge length 6√2 are coordinate permutations:

(±1,±1,±3,±3,±3,±3,±3)

with an odd number of plus signs.

Images

It can be visualized as a 2-dimensional orthogonal projections, for example the a D7 Coxeter plane, containing 12-gonal symmetry. Most visualizations in symmetric projections will contain overlapping vertices, so the colors of the vertices are changed based on how many vertices are at each projective position, here shown with red color for no overlaps.

orthographic projections
Coxeter
plane		 B7 D7 D6
Graph
Dihedral
symmetry		 [14/2] [12] [10]
Coxeter plane D5 D4 D3
Graph
Dihedral
symmetry		 [8] [6] [4]
Coxeter
plane		 A5 A3
Graph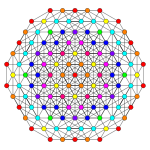
Dihedral
symmetry		 [6] [4]

Related polytopes

Dimensional family of cantic n-cubes
n345678
Symmetry
[1+,4,3n-2]		 [1+,4,3]
= [3,3]		 [1+,4,32]
= [3,31,1]		 [1+,4,33]
= [3,32,1]		 [1+,4,34]
= [3,33,1]		 [1+,4,35]
= [3,34,1]		 [1+,4,36]
= [3,35,1]
Cantic
figure
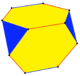Coxeter
=
=
=
=
=
=
Schläfli h2{4,3} h2{4,32} h2{4,33} h2{4,34} h2{4,35} h2{4,36}

There are 95 uniform polytopes with D6 symmetry, 63 are shared by the B6 symmetry, and 32 are unique:

Notes

  1. ↑ Klitzing, (x3x3o *b3o3o3o3o - thesa)

References

External links

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family An Bn I2(p) / Dn E6 / E7 / E8 / E9 / E10 / F4 / G2 Hn
Regular polygon Triangle Square p-gon Hexagon Pentagon
Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron
Uniform 4-polytope 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell
Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube
Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221
Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321
Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421
Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube
Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube
Uniform n-polytope n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds
This article is issued from Wikipedia - version of the 4/23/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.