List of isotoxal polyhedra and tilings
In geometry, isotoxal polyhedra and tilings are edge-transitive. An isotoxal polyhedron or tiling must be either isogonal (vertex-transitive) or isohedral (face-transitive) or both. Regular polyhedra are isohedral (face-transitive), isogonal (vertex-transitive) and isotoxal. Quasiregular polyhedra are isogonal and isotoxal, but not isohedral; their duals are isohedral and isotoxal, but not isogonal.
Convex isotoxal polyhedra
There are nine convex isotoxal polyhedra formed from the Platonic solids. The vertex figures of the quasiregular forms are rectangles, and the vertex figure of the duals of the quasiregular are rhombi.
| Form | Regular | Dual regular | Quasiregular | Quasiregular dual |
|---|---|---|---|---|
| Wythoff symbol | q | 2 p | p | 2 q | 2 | p q | |
| Vertex configuration | pq | qp | p.q.p.q | |
| p=3 q=3 |
 Tetrahedron {3,3} 3 | 2 3 |
 Tetrahedron {3,3} 3 | 2 3 |
 Tetratetrahedron (Octahedron) 2 | 3 3 |
 Cube (Rhombic hexahedron) |
| p=4 q=3 |
 Cube {4,3} 3 | 2 4 |
 Octahedron {3,4} 4 | 2 3 |
 Cuboctahedron 2 | 3 4 |
 Rhombic dodecahedron |
| p=5 q=3 |
 Dodecahedron {5,3} 3 | 2 5 |
 Icosahedron {3,5} 5 | 2 3 |
 Icosidodecahedron 2 | 3 5 |
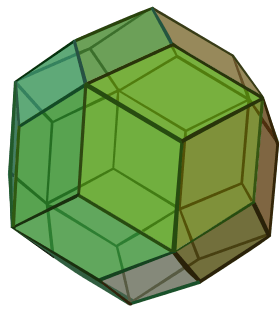 Rhombic triacontahedron |
Isotoxal star-polyhedra
5 nonconvex hemipolyhedra are based on the octahedron, cuboctahedron and icosidodecahedron:
| Form | Quasiregular | Quasiregular dual |
|---|---|---|
| p= q= |
  Tetrahemihexahedron |
 Tetrahemihexacron |
| p= q= |
  Cubohemioctahedron |
 Hexahemioctacron |
  Octahemioctahedron |
 Octahemioctacron | |
| p= q= |
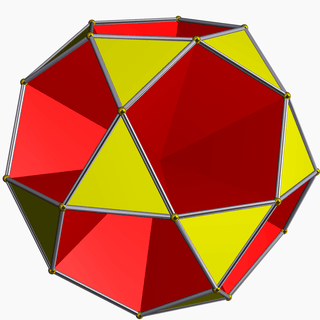  Small icosihemidodecahedron |
 Small icosihemidodecacron |
  Small dodecahemidodecahedron |
 Small dodecahemidodecacron |
There are 12 formed by the Kepler–Poinsot polyhedra, including four hemipolyhedra:
| Form | Regular | Dual regular | Quasiregular | Quasiregular dual |
|---|---|---|---|---|
| Wythoff symbol | q | 2 p | p | 2 q | 2 | p q | |
| Vertex configuration | pq | qp | p.q.p.q | |
| p=5/2 q=3 |
  Great stellated dodecahedron {5/2,3}
|
 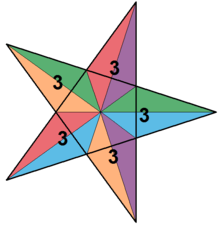 Great icosahedron {3,5/2}
|
  Great icosidodecahedron 2 | 3 5/2 |
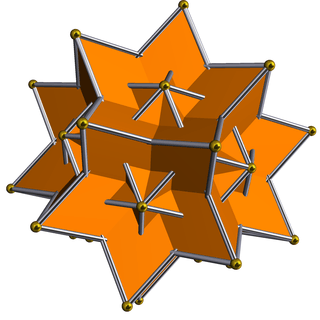 Great rhombic triacontahedron |
  Great icosihemidodecahedron |
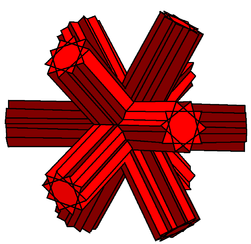 Great icosihemidodecacron | |||
  Great dodecahemidodecahedron |
 Great dodecahemidodecacron | |||
| p=5/2 q=5 |
  Small stellated dodecahedron {5/2,5}
|
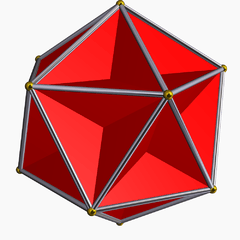  Great dodecahedron {5,5/2}
|
  Dodecadodecahedron 2 | 5 5/2 |
 Medial rhombic triacontahedron |
  Small icosihemidodecahedron |
 Small dodecahemicosacron | |||
  Great dodecahemidodecahedron |
 Great dodecahemicosacron |
There are a final three quasiregular (3 | p q) star polyhedra and their duals:
| Quasiregular | Quasiregular dual |
|---|---|
| 3 | p q | |
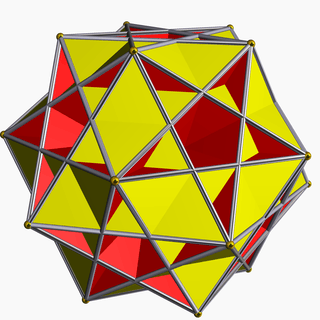  Great ditrigonal icosidodecahedron 3/2 | 3 5 |
 Great triambic icosahedron |
  Ditrigonal dodecadodecahedron 3 | 5/3 5 |
 Medial triambic icosahedron |
  Small ditrigonal icosidodecahedron 3 | 5/2 3 |
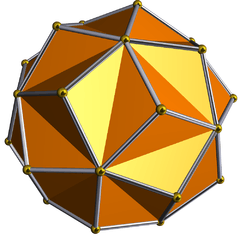 Small triambic icosahedron |
Isotoxal tilings of the Euclidean plane
There are 5 polygonal tilings of the Euclidean plane that are isotoxal. (The self-dual square tiling recreates itself in all four forms.)
| Regular | Dual regular | Quasiregular | Quasiregular dual |
|---|---|---|---|
 Hexagonal tiling {6,3} 6 | 2 3 |
 Triangular tiling {3,6} 3 | 2 3 |
 Trihexagonal tiling 2 | 3 6 |
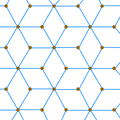 Rhombille tiling |
 Square tiling {4,4} 4 | 2 4 |
 Square tiling {4,4} 2 | 4 4 |
 Square tiling {4,4} 4 | 2 4 |
 Square tiling {4,4} |
Isotoxal tilings of the hyperbolic plane
There are infinitely many isotoxal polygonal tilings of the hyperbolic plane, including the Wythoff constructions from the regular hyperbolic tilings {p,q}, and non-right (p q r) groups.
Here are six (p q 2) families, each with two regular forms, and one quasiregular form. All have rhombic duals of the quasiregular form, but only one is shown:
| [p,q] | {p,q} | {q,p} | r{p,q} | Dual r{p,q} |
|---|---|---|---|---|
| Coxeter-Dynkin | ||||
| [7,3] |  {7,3} |
 {3,7} |
 r{7,3} |
 |
| [8,3] |  {8,3} |
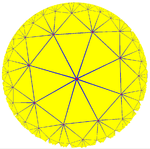 {3,8} |
 r{8,3} |
 |
| [5,4] |  {5,4} |
 {4,5} |
 r{5,4} |
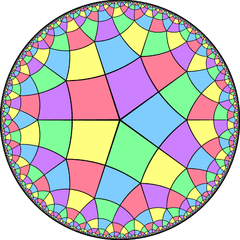 |
| [6,4] |  {6,4} |
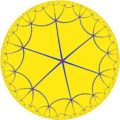 {4,6} |
 r{6,4} |
 |
| [8,4] |  {8,4} |
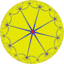 {4,8} |
 r{8,3} |
 |
| [5,5] |  {5,5} |
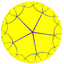 {5,5} |
 r{5,5} |
 |
Here's 3 example (p q r) families, each with 3 quasiregular forms. The duals are not shown, but have isotaxal hexagonal and octagonal faces.
| Coxeter-Dynkin | |||
|---|---|---|---|
| (4 3 3) |  3 | 4 3 |
 3 | 4 3 |
 4 | 3 3 |
| (4 4 3) |  4 | 4 3 |
 3 | 4 4 |
 4 | 4 3 |
| (4 4 4) |  4 | 4 4 |
 4 | 4 4 |
 4 | 4 4 |
Isotoxal tilings of the sphere
All isotoxal polyhedra listed above can be made as isotoxal tilings of the sphere.
In addition as spherical tilings, there are two other families which are degenerate as polyhedra. Even ordered hosohedron can semiregular, alternating two lunes, and thus isotoxal.
- hosohedron {2,q}
- dihedron {p,2}
References
- Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, p. 371 Transitivity
- Grünbaum, Branko; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (6.4 Isotoxal tilings, 309–321)
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246: 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446
