Snub square tiling
| Snub square tiling | |
|---|---|
 | |
| Type | Semiregular tiling |
| Vertex configuration | 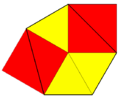 3.3.4.3.4 |
| Schläfli symbol | s{4,4} sr{4,4} or |
| Wythoff symbol | | 4 4 2 |
| Coxeter diagram | |
| Symmetry | p4g, [4+,4], (4*2) |
| Rotation symmetry | p4, [4,4]+, (442) |
| Bowers acronym | Snasquat |
| Dual | Cairo pentagonal tiling |
| Properties | Vertex-transitive |
In geometry, the snub square tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. Its Schläfli symbol is s{4,4}.
Conway calls it a snub quadrille, constructed by a snub operation applied to a square tiling (quadrille).
There are 3 regular and 8 semiregular tilings in the plane.
Uniform colorings
There are two distinct uniform colorings of a snub square tiling. (Naming the colors by indices around a vertex (3.3.4.3.4): 11212, 11213.)
| Coloring |  11212 |
 11213 |
|---|---|---|
| Symmetry | 4*2, [4+,4], (p4g) | 442, [4,4]+, (p4) |
| Schläfli symbol | s{4,4} | sr{4,4} |
| Wythoff symbol | | 4 4 2 | |
| Coxeter diagram |
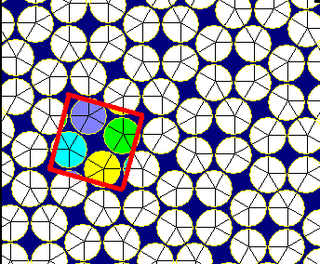
Circle packing
The snub square tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing number).[1]
Wythoff construction
The snub square tiling can be constructed as a snub operation from the square tiling, or as an alternate truncation from the truncated square tiling.
An alternate truncation deletes every other vertex, creating a new triangular faces at the removed vertices, and reduces the original faces to half as many sides. In this case starting with a truncated square tiling with 2 octagons and 1 square per vertex, the octagon faces into squares, and the square faces degenerate into edges and 2 new triangles appear at the truncated vertices around the original square.
If the original tiling is made of regular faces the new triangles will be isosceles. Starting with octagons which alternate long and short edge lengths will produce a snub tiling with perfect equilateral triangle faces.
Example:
 Regular octagons alternately truncated |
→ (Alternatetruncation) |
 Isosceles triangles (Nonuniform tiling) |
 Nonregular octagons alternately truncated |
→ (Alternatetruncation) |
 Equilateral triangles |
Related tilings
This tiling is related to the elongated triangular tiling which also has 3 triangles and two squares on a vertex, but in a different order.
The snub square tiling can be seen related to this 3-colored square tiling, with the yellow and red squares being twisted rigidly and the blue tiles being distorted into rhombi and then bisected into two triangles.

Related polyhedra and tilings
The snub square tiling is similar to the elongated triangular tiling with vertex configuration 3.3.3.4.4, and two 2-uniform dual tilings and 2 3-uniform duals which mix the two types of pentagons:[2][3]
 3.3.3.4.4 |
 3.3.4.3.4 |
| Related tilings of triangles and squares | ||
|---|---|---|
| snub square tiling | 2-uniform | |
| p4g, (4*2) | p2, (2222) | cmm, (2*22) |
 3.3.4.3.4 |
 (3.3.3.4.4; 3.3.4.3.4) |
 (3.3.3.4.4; 3.3.4.3.4) |
| Elongated triangular tiling | 3-uniform | |
| cmm, (2*22) | p2, (2222) | |
 3.3.3.4.4 |
 (3.3.3.4.4; 3.3.4.3.4) |
 (3.3.3.4.4; 3.3.4.3.4) |
The snub square tiling is third in a series of snub polyhedra and tilings with vertex figure 3.3.4.3.n.
| 4n2 symmetry mutations of snub tilings: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
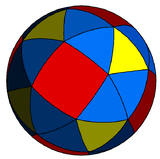
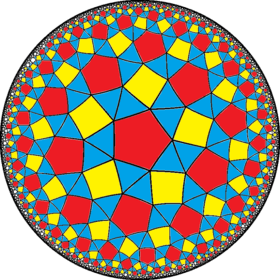
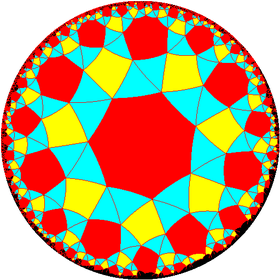
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Snub figures |
 |
 |
 |
 |
 |
 |
 |
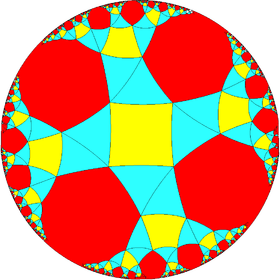 |
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Gyro figures |
 |
 |
 |
 |
||||
| Config. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
The snub square tiling is third in a series of snub polyhedra and tilings with vertex figure 3.3.n.3.n.
| 4n2 symmetry mutations of snub tilings: 3.3.n.3.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracompact | |||||||
| 222 | 322 | 442 | 552 | 662 | 772 | 882 | ∞∞2 | ||||
| Snub figures |
 |
 |
 |
 |
 |
 |
 |
 | |||
| Config. | 3.3.2.3.2 | 3.3.3.3.3 | 3.3.4.3.4 | 3.3.5.3.5 | 3.3.6.3.6 | 3.3.7.3.7 | 3.3.8.3.8 | 3.3.∞.3.∞ | |||
| Gyro figures |
 |
 |
 |
 | |||||||
| Config. | V3.3.2.3.2 | V3.3.3.3.3 | V3.3.4.3.4 | V3.3.5.3.5 | V3.3.6.3.6 | V3.3.7.3.7 | V3.3.8.3.8 | V3.3.∞.3.∞ | |||
| Uniform tilings based on square tiling symmetry | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,4], (*442) | [4,4]+, (442) | [4,4+], (4*2) | |||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| {4,4} | t{4,4} | r{4,4} | t{4,4} | {4,4} | rr{4,4} | tr{4,4} | sr{4,4} | s{4,4} | |||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.4.4.4 | V4.8.8 | V3.3.4.3.4 | ||||
See also
| Wikimedia Commons has media related to Uniform tiling 3-3-4-3-4. |
- List of uniform planar tilings
- Snub square prismatic honeycomb
- Tilings of regular polygons
- Elongated triangular tiling
References
- ↑ Order in Space: A design source book, Keith Critchlow, p.74-75, circle pattern C
- ↑ Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
- ↑ http://www.uwgb.edu/dutchs/symmetry/uniftil.htm
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- Klitzing, Richard. "2D Euclidean tilings s4s4s - snasquat - O10".
- Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p38
- Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–56, dual p. 115
